quantitative research hypothesis testing

• Teesside University Student & Library Services
• Learning Hub Group

Quantitative data collection and analysis

• Testing hypotheses
• Quantitative data collection
• Averages and percentiles
• Measures of Spread or Dispersion
• Samples and population
• Statistical tests - parametric
• Statistical tests - non-parametric
• Probability
• Reliability and Validity
• Analysing relationships
• Useful Books

Testing Hypotheses

• What is a hypothesis?
• Significance testing
• One-tailed or two-tailed?
• Degrees of freedom

A hypothesis is a statement that we are trying to prove or disprove. It is used to express the relationship between variables  and whether this relationship is significant. It is specific and offers a prediction on the results of your research question.

Your research question  will lead you to developing a hypothesis, this is why your research question needs to be specific and clear.

The hypothesis will then guide you to the most appropriate techniques you should use to answer the question. They reflect the literature and theories on which you basing them. They need to be testable (i.e. measurable and practical).

Null hypothesis  (H 0 ) is the proposition that there will not be a relationship between the variables you are looking at. i.e. any differences are due to chance). They always refer to the population. (Usually we don't believe this to be true.)

e.g. There is  no difference in instances of illegal drug use by teenagers who are members of a gang and those who are not..

Alternative hypothesis  (H A ) or ( H 1 ):  this is sometimes called the research hypothesis or experimental hypothesis. It is the proposition that there will be a relationship. It is a statement of inequality between the variables you are interested in. They always refer to the sample. It is usually a declaration rather than a question and is clear, to the point and specific.

e.g. The instances of illegal drug use of teenagers who are members of a gang  is different than the instances of illegal drug use of teenagers who are not gang members.

A non-directional research hypothesis - reflects an expected difference between groups but does not specify the direction of this difference (see two-tailed test).

A directional research hypothesis - reflects an expected difference between groups but does specify the direction of this difference. (see one-tailed test)

e.g. The instances of illegal drug use by teenagers who are members of a gang will be higher t han the instances of illegal drug use of teenagers who are not gang members.

Then the process of testing is to ascertain which hypothesis to believe. 

It is usually easier to prove something as untrue rather than true, so looking at the null hypothesis is the usual starting point.

The process of examining the null hypothesis in light of evidence from the sample is called significance testing . It is a way of establishing a range of values in which we can establish whether the null hypothesis is true or false.

The debate over hypothesis testing

There has been discussion over whether the scientific method employed in traditional hypothesis testing is appropriate.  

See below for some articles that discuss this:

• Gill, J. (1999) 'The insignificance of null hypothesis testing',  Politics Research Quarterly , 52(3), pp. 647-674.
• Wainer, H. and Robinson, D.H. (2003) 'Shaping up the practice of null hypothesis significance testing',  Educational Researcher, 32(7), pp.22-30.
• Ferguson, C.J. and Heener, M. (2012) ' A vast graveyard of undead theories: publication bias and psychological science's aversion to the null' , Perspectives on Psychological Science , 7(6), pp.555-561.

Taken from: Salkind, N.J. (2017)  Statistics for people who (think they) hate statistics. 6th edn. London: SAGE pp. 144-145.

• Null hypothesis - a simple introduction (SPSS)

A significance level defines the level when your sample evidence contradicts your null hypothesis so that your can then reject it. It is the probability of rejecting the null hypothesis when it is really true.

e.g. a significance level of 0.05 indicates that there is a 5% (or 1 in 20) risk of deciding that there is an effect when in fact there is none.

The lower the significance level that you set,  then the evidence from the sample has to be stronger to be able to reject the null hypothesis.

N.B.  - it is important that you set the significance level before you carry out your study and analysis.

Using Confidence Intervals

I t is possible to test the significance of your null hypothesis using Confidence Interval (see under samples and populations tab).

- if the range lies outside our predicted null hypothesis value we can reject it and accept the alternative hypothesis  

The test statistic

This is another commonly used statistic

• Write down your null and alternative hypothesis
• Find the sample statistic (e.g.the mean of your sample)
• Calculate the test statistic Z score (see under Measures of spread or dispersion and Statistical tests - parametric). In this case the sample mean is compared to the population mean (assumed from the null hypothesis) and the standard error (see under Samples and population) is used rather than the standard deviation.
• Compare the test statistic with the critical values (e.g. plus or minus 1.96 for 5% significance)
• Draw a conclusion about the hypotheses - does the calculated z value lies in this critical range i.e. above 1.96 or below -1.96? If it does we can reject the null hypothesis. This would indicate that the results are significant (or an effect has been detected) - which means that if there were no difference in the population then getting a result that you have observed would be highly unlikely therefore you can reject the null hypothesis.

Type I error  - this is the chance of wrongly rejecting the null hypothesis even though it is actually true, e.g. by using a 5% p  level you would expect the null hypothesis to be rejected about 5% of the time when the null hypothesis is true. You could set a more stringent p  level such as 1% (or 1 in 100) to be more certain of not seeing a Type I error. This, however, makes more likely another type of error (Type II) occurring.

Type II error  - this is where there is an effect, but the  p  value you obtain is non-significant hence you don’t detect this effect.

• Statistical significance - what does it really mean?
• Statistical tables

One-tailed tests - where we know in which direction (e.g. larger or smaller) the difference between sample and population will be. It is a directional hypothesis.

Two-tailed tests - where we are looking at whether there is a difference between sample and population. This difference could be larger or smaller. This is a non-directional hypothesis.

If the difference is in the direction you have predicted (i.e. a one-tailed test) it is easier to get a significant result. Though there are arguments against using a one-tailed test (Wright and London, 2009, p. 98-99)*

*Wright, D. B. & London, K. (2009)  First (and second) steps in statistics . 2nd edn. London: SAGE.

N.B. - think of the ‘tails’ as the regions at the far-end of a normal distribution. For a two-tailed test with significance level of 0.05% then 0.025% of the values would be at one end of the distribution and the other 0.025% would be at the other end of the distribution. It is the values in these ‘critical’ extreme regions where we can think about rejecting the null hypothesis and claim that there has been an effect.

Degrees of freedom ( df)  is a rather difficult mathematical concept, but is needed to calculate the signifcance of certain statistical tests, such as the t-test, ANOVA and Chi-squared test.

It is broadly defined as the number of "observations" (pieces of information) in the data that are free to vary when estimating statistical parameters. (Taken from Minitab Blog ).

The higher the degrees of freedom are the more powerful and precise your estimates of the parameter (population) will be.

Typically, for a 1-sample t-test it is considered as the number of values in your sample minus 1.

For chi-squared tests with a table of rows and columns the rule is:

(Number of rows minus 1) times (number of columns minus 1)

Any accessible example to illustrate the principle of degrees of freedom using chocolates.

• You have seven chocolates in a box, each being a different type, e.g. truffle, coffee cream, caramel cluster, fudge, strawberry dream, hazelnut whirl, toffee. 
• You are being good and intend to eat only one chocolate each day of the week.
• On the first day, you can choose to eat any one of the 7 chocolate types  - you have a choice from all 7.
• On the second day, you can choose from the 6 remaining chocolates, on day 3 you can choose from 5 chocolates, and so on.
• On the sixth day you have a choice of the remaining 2 chocolates you haven't ate that week.
• However on the seventh day - you haven't really got any choice of chocolate - it has got to be the one you have left in your box.
• You had 7-1 = 6 days of “chocolate” freedom—in which the chocolate you ate could vary!
• << Previous: Samples and population
• Next: Statistical tests - parametric >>
• Last Updated: Aug 1, 2024 3:26 PM
• URL: https://libguides.tees.ac.uk/quantitative

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Quantitative Data Analysis

5 Hypothesis Testing in Quantitative Research

Mikaila Mariel Lemonik Arthur

Statistical reasoning is built on the assumption that data are normally distributed , meaning that they will be distributed in the shape of a bell curve as discussed in the chapter on Univariate Analysis . While real life often—perhaps even usually—does not resemble a bell curve, basic statistical analysis assumes that if all possible random samples from a population were drawn and the mean taken from each sample, the distribution of sample means, when plotted on a graph, would be normally distributed (this assumption is called the Central Limit Theorem ). Given this assumption, we can use the mathematical techniques developed for the study of probability to determine the likelihood that the relationships or patterns we observe in our data occurred due to random chance rather than due some actual real-world connection, which we call statistical significance.

Statistical significance is not the same as practical significance. The fact that we have determined that a given result is unlikely to have occurred due to random chance does not mean that this given result is important, that it matters, or that it is useful. Similarly, we might observe a relationship or result that is very important in practical terms, but that we cannot claim is statistically significant—perhaps because our sample size is too small, for instance. Such a result might have occurred by chance, but ignoring it might still be a mistake. Let’s consider some examples to make this a bit clearer. Assume we were interested in the impacts of diet on health outcomes and found the statistically significant result that people who eat a lot of citrus fruit end up having pinky fingernails that are, on average, 1.5 millimeters longer than those who tend not to eat any citrus fruit. Should anyone change their diet due to this finding? Probably not, even those it is statistically significant. On the other hand, if we found that the people who ate the diets highest in processed sugar died on average five years sooner than those who ate the least processed sugar, even in the absence of a statistically significant result we might want to advise that people consider limiting sugar in their diet. This latter result has more practical significance (lifespan matters more than the length of your pinky fingernail) as well as a larger effect size or association (5 years of life as opposed to 1.5 millimeters of length), a factor that will be discussed in the chapter on association .

While people generally use the shorthand of “the likelihood that the results occurred by chance” when talking about statistical significance, it is actually a bit more complicated than that. What statistical significance is really telling us is the likelihood (or probability ) that a result equal to or more “extreme [1] ” is true in the real world, rather than our results having occurred due to random chance or sampling error . Testing for statistical significance, then, requires us to understand something about probability.

A Brief Review of Probability

You might remember having studied probability in a math class, with questions about coin flips or drawing marbles out of a jar. Such exercises can make probability seem very abstract. But in reality, computations of probability are deeply important for a wide variety of activities, ranging from gambling and stock trading to weather forecasts and, yes, statistical significance.

Probability is represented as a proportion (or decimal number) somewhere between 0 and 1. At 0, there is absolutely no likelihood that the event or pattern of interest would occur; at 1, it is absolutely certain that the event or pattern of interest will occur. We indicate that we are talking about probability by using the symbol [latex]p[/latex]. For example, if something has a 50% chance of occurring, we would write [latex]p=0.5[/latex] or [latex]\frac {1}{2}[/latex]. If we want to represent the likelihood of something not occurring, we can write [latex]1-p[/latex].

Check your thinking: Assume you were flipping coins, and you called heads. The probability of getting heads on a coin flip using a fair coin (in other words, a normal coin that has not been weighted to bias the result) is 0.5. Thus, in 50% of coin flips you should get heads. Consider the following probability questions and write down your answers so you can check them against the discussion below.

• Imagine you have flipped the coin 29 times and you have gotten heads each time. What is the probability you will get heads on flip 30?
• What is the probability that you will get heads on all of the first five coin flips?
• What is the probability that you will get heads on at least one of the first five coin flips?

There are a few basic concepts from the mathematical study of probability that are important for beginner data analysts to know, and we will review them here.

Probability over Repeated Trials : The probability of the outcome of interest is the same in each trial or test, regardless of the results of the prior test. So, if we flip a coin 29 times and get heads each time, what happens when we flip it the 29th time? The probability of heads is still 0.5! The belief that “this time it must be tails because it has been heads so many times” or “this coin just wants to come up heads” is simply superstition, and—assuming a fair coin—the results of prior trials do not influence the results of this one.

Probability of Multiple Events : The probability that the outcome of interest will occur repeatedly across multiple trials is the product [2] of the probability of the outcome on each individual trial. This is called the multiplication theorem . Thinking about the multiplication theorem requires that we keep in mind the fact that when we multiply decimal numbers together, those numbers get smaller— thus, the probability that a series of outcomes will occur is smaller than the probability of any one of those outcomes occurring on its own. So, what is the probability that we will get heads on all five of our coin flips? Well, to figure that out, we need to multiply the probability of getting heads on each of our coin flips together. The math looks like this (and produces a very small probability indeed):

[latex]\frac {1}{2} \cdot \frac {1}{2} \cdot \frac {1}{2} \cdot \frac {1}{2} \cdot \frac {1}{2} = 0.03125[/latex]

Probability of One of Many Events : Determining the probability that the outcome of interest will occur on at least one out of a series of events or repeated trials is a little bit more complicated. Mathematicians use the addition theorem to refer to this, because the basic way to calculate it is to calculate the probability of each sequence of events (say, heads-heads-heads, heads-heads-tails, heads-tails-heads, and so on) and add them together. But the greater the number of repeated trials, the more complicated that gets, so there is a simpler way to do it. Consider that the probability of getting  no heads is the same as the probability of getting all tails (which would be the same as the probability of getting all heads that we calculated above). And the only circumstance in which we would not have at least one flip resulting in heads would be a circumstance in which all flips had resulted in tails. Therefore, what we need to do in order to calculate the probability that we get at least one heads is to subtract the probability that we get no heads from 1—and as you can imagine, this procedure shows us that the probability of the outcome of interest occurring at least once over repeated trials is higher than the probability of the occurrence on any given trial. The math would look like this:

[latex]1- (\frac{1}{2})^5=0.9688[/latex]

So why is this digression into the math of probability important? Well, when we test for statistical significance, what we are really doing is determining the probability that the outcome we observed—or one that is more extreme than that which we observed—occurred by chance. We perform this analysis via a procedure called Null Hypothesis Significance Testing.

Null Hypothesis Significance Testing

Null hypothesis significance testing , or NHST , is a method of testing for statistical significance by comparing observed data to the data we would expect to see if there were no relationship between the variables or phenomena in question. NHST can take a little while to wrap one’s head around, especially because it relies on a logic of double negatives: first, we state a hypothesis we believe not to be true (there is no relationship between the variables in question) and then, we look for evidence that disconfirms this hypothesis. In other words, we are assuming that there is no relationship between the variables—even though our research hypothesis states that we think there is a relationship—and then looking to see if there is any evidence to suggest there is not no relationship. Confusing, right?

So why do we use the null hypothesis significance testing approach?

• The null hypothesis—that there is no relationship between the variables we are exploring—would be what we would generally accept as true in the absence of other information,
• It means we are assuming that differences or patterns occur due to chance unless there is strong evidence to suggest otherwise,
• It provides a benchmark for comparing observed outcomes, and
• It means we are searching for evidence that disconforms our hypothesis, making it less likely that we will accept a conclusion that turns out to be untrue.

Thus, NHST helps us avoid making errors in our interpretation of the result. In particular, it helps us avoid Type 2 error , as discussed in the chapter on Bivariate Analyses . As a reminder, Type 2 error is error where you accept a hypothesis as true when in fact it was false (while Type 1 error is error where you reject the hypothesis when in fact it was true). For example, you are making a Type 1 error if you decide not to study for a test because you assume you are so bad at the subject that studying simply cannot help you, when in fact we know from research that studying does lead to higher grades. And you are making a Type 2 error if your boss tells you that she is going to promote you if you do enough overtime and you then work lots of overtime in response, when actually your boss is just trying to make you work more hours and already had someone else in mind to promote.

We can never remove all sources of error from our analyses, though larger sample sizes help reduce error. Looking at the formula for computing standard error , we can see that the standard error ([latex]SE[/latex]) would get smaller as the sample size ([latex]N[/latex]) gets larger. Note: σ is the symbol we use to represent standard deviation.

[latex]SE = \frac{\sigma}{\sqrt N}[/latex]

Besides making our samples larger, another thing that we can do is that we can choose whether we are more willing to accept Type 1 error or Type 2 error and adjust our strategies accordingly. In most research, we would prefer to accept more Type 1 error, because we are more willing to miss out on a finding than we are to make a finding that turns out later to be inaccurate (though, of course, lots of research does eventually turn out to be inaccurate).

Performing NHST

Performing NHST requires that our data meet several assumptions:

• Our sample must be a random sample—statistical significance testing and other inferential and explanatory statistical methods are generally not appropriate for non-random samples [3] —as well as representative and of a sufficient size (see the Central Limit Theorem above).
• Observations must be independent of other observations, or else additional statistical manipulation must be performed. For instance, a dataset of data about siblings would need to be handled differently due to the fact that siblings affect one another, so data on each person in the dataset is not truly independent.
• You must determine the rules for your significance test, including the level of uncertainty you are willing to accept (significance level) and whether or not you are interested in the direction of the result (one-tailed versus two-tailed tests, to be discussed below), in advance of performing any analysis.
• The number of significance tests you run should be limited, because the more tests you run, the greater the likelihood that one of your tests will result in an error. To make this more clear, if you are willing to accept a 5% probability that you will make the error of accepting a hypothesis as true when it is really false, and you run 20 tests, one of those tests (5% of them!) is pretty likely to have produced an incorrect result.

If our data has met these assumptions, we can move forward with the process of conducting an NHST. This requires us to make three decisions: determining our null hypothesis , our confidence level (or acceptable significance level), and whether we will conduct a one-tailed or a two-tailed test. In keeping with Assumption 3 above, we must make these decisions before performing our analysis. The null hypothesis is the hypothesis that there is no relationship between the variables in question. So, for example, if our research hypothesis was that people who spend more time with their friends are happier, our null hypothesis would be that there is no relationship between how much time people spend with their friends and their happiness.

Our confidence level is the level of risk we are willing to accept that our results could have occurred by chance. Typically, in social science research, researchers use p<0.05 (we are willing to accept up to a 5% risk that our results occurred by chance), p<0.01 (we are willing to accept up to a 1% risk that our results occurred by chance), and/or p<0.001 (we are willing to accept up to a 0.1% risk that our results occurred by chance). P, as was noted above, is the mathematical notation for probability, and that’s why we use a p-value to indicate the probability that our results may have occurred by chance. A higher p-value increases the likelihood that we will accept as accurate a result that really occurred by chance; a lower p-value increases the likelihood that we will assume a result occurred by chance when actually it was real. Remember, what the p-value tells us is not the probability that our own research hypothesis is true, but rather this: assuming that the null hypothesis is correct, what is the probability that the data we observed—or data more extreme than the data we observed—would have occurred by chance.

Whether we choose a one-tailed or a two-tailed test tells us what we mean when we say “data more extreme than.” Remember that normal curve? A two-tailed test is agnostic as to the direction of our results—and many of the most common tests for statistical significance that we perform, like the Chi square, are two-tailed by default. However, if you are only interested in a result that occurs in a particular direction, you might choose a one-tailed test. For instance, if you were testing a new blood pressure medication, you might only care if the blood pressure of those taking the medication is significantly lower than those not taking the medication—having blood pressure significantly higher would not be a good or helpful result, so you might not want to test for that.

Having determined the parameters for our analysis, we then compute our test of statistical significance. There are different tests of statistical significance for different variables (for example, the Chi square discussed in the chapter on bivariate analyses ), as you will see in other chapters of this text, but all of them produce results in a similar format. We then compare this result to the p value we already selected. If the p value produced by our analysis is lower than the confidence level we selected, we can reject the null hypothesis, as the probability that our result occurred by chance is very low. If, on the other hand, the p value produced by our analysis is higher than the confidence level we selected, we fail to reject the null hypothesis, as the probability that our result occurred by chance is too high to accept. Keep in mind this is what we do even when the p value produced by our analysis is quite close to the threshold we have selected. So, for instance, if we have selected the confidence level of p<0.05 and the p value produced by our analysis is p=0.0501, we still fail to reject the null hypothesis and proceed as if there is not any support for our research hypothesis.

Thus, the process of null hypothesis significance testing proceeds according to the following steps:

• Determine the null hypothesis
• Set the confidence level and whether this will be a one-tailed or two-tailed test
• Compute the test value for the appropriate significance test
• Compare the test value to the critical value of that test statistic for the confidence level you selected
• Determine whether or not to reject the null hypothesis

Your statistical analysis software will perform steps 3 and 4 for you (before there was computer software to do this, researchers had to do the calculations by hand and compare their results to figures on published tables of critical values). But you as the researcher must perform steps 1, 2, and 5 yourself.

Confidence Intervals & Margins of Error

When talking about statistical significance, some researchers also use the terms confidence intervals and margins of error . Confidence intervals are ranges of probabilities within which we can assume the true population parameter lies. Most typically, analysts aim for 95% confidence intervals, meaning that in 95 out of 100 cases, the population parameter will lie within the upper and lower levels specified by your confidence interval. These are calculated by your statistics software as well. The margin of error, then, is the range of values within the confidence interval. So, for instance, a 2021 survey of Americans conducted by the Robert Wood Johnson Foundation and the Harvard T.H. Chan School of Public Health found that 71% of respondents favor substantially increasing federal spending on public health programs. This poll had a 95% confidence interval with a +/- 3.6 margin of error. What this tells us is that there is a 95% probability (19 in 20) that between 67.4% (71-3.6) and 74.6% (71+3.6) of Americans favored increasing federal public health spending at the time the poll was conducted. When a figure reflects an overwhelming majority, such as this one, the margin of error may seem of little relevance. But consider a similar poll with the same margin of error that sought to predict support for a political candidate and found that 51.5% of people said they would vote for that candidate. In that case, we would have found that there was a 95% probability that between 47.9% and 55.1% of people intended to vote for the candidate—which means the race is total tossup and we really would have no idea what to expect. For some people, thinking in terms of confidence intervals and margins of error is easier to understand than thinking in terms of p values; confidence intervals and margins of error are more frequently used in analyses of polls while p values are found more often in academic research. But basically, both approaches are doing the same fundamental analysis—they are determining the likelihood that the results we observed or a similarly-meaningful result would have occurred by chance.

What Does Significance Testing Tell Us?

One of the most important things to remember about significance testing is that, while the word “significance” is used in ordinary speech to mean importance, significance testing does not tell us whether our results are important—or even whether they are interesting. A full understanding of the relationship between a given set of variables requires looking at statistical significance as well as association and the theoretical importance of the findings. Table 1 provides a perspective on using the combination of significance and association to determine how important the results of statistical analysis are—but even using Table 1 as a guide, evaluating findings based on theoretical importance remains key. So: make sure that when you are conducting analyses, you avoid being misled into assuming that significant results are sufficient for making broad claims about the importance and meaning of results. And remember as well that significance only tells us the likelihood that the pattern of relationships we observe occurred by chance—not whether that pattern is causal. For, after all, quantitative research can never eliminate all plausible alternative explanations for the phenomenon in question (one of the three elements of causation, along with association and temporal order).

• Getting 7 heads on 7 coin flips
• Getting 5 heads on 7 coin flips
• Getting 1 head on 10 coin flips

Then check your work using the Coin Flip Probability Calculator .

• As the advertised hourly pay for a job goes up, the number of job applicants increases.
• Teenagers who watch more hours of makeup tutorial videos on TikTok have, on average, lower self-esteem.
• Couples who share hobbies in common are less likely to get divorced.
• Assume a research conducted a study that found that people wearing green socks type on average one word per minute faster than people who are not wearing green socks, and that this study found a p value of p<0.01. Is this result statistically significant? Is this result practically significant? Explain your answers.
• If we conduct a political poll and have a 95% confidence interval and a margin of error of +/- 2.3%, what can we conclude about support for Candidate X if 49.3% of respondents tell us they will vote for Candidate X? If 24.7% do? If 52.1% do? If 83.7% do?
• One way to think about this is to imagine that your result has been plotted on a bell curve. Statistical significance tells us the probability that the "real" result—the thing that is true in the real world and not due to random chance—is at the same point as or further along the skinny tails of the bell curve than the result we have plotted. ↵
• In other words, what you get when you multiply. ↵
• They also are not appropriate for censuses—but you do not need inferential statistics in a census because you are looking at the entire population rather than a sample, so you can simply describe the relationships that do exist. ↵

A distribution of values that is symmetrical and bell-shaped.

A graph showing a normal distribution—one that is symmetrical with a rounded top that then falls away towards the extremes in the shape of a bell

The sum of all the values in a list divided by the number of such values.

The theorem that states that if you take a series of sufficiently large random samples from the population (replacing people back into the population so they can be reselected each time you draw a new sample), the distribution of the sample means will be approximately normally distributed.

A statistical measure that suggests that sample results can be generalized to the larger population, based on a low probability of having made a Type 1 error.

How likely something is to happen; also, a branch of mathematics concerned with investigating the likelihood of occurrences.

Measurement error created due to the fact that even properly-constructed random samples are do not have precisely the same characteristics as the larger population from which they were drawn.

The theorem in probability about the likelihood of a given outcome occurring repeatedly over multiple trials; this is determined by multiplying the probabilities together.

The theorem addressing the determination of the probability of a given outcome occurring at least once across a series of trials; it is determined by adding the probability of each possible series of outcomes together.

A method of testing for statistical significance in which an observed relationship, pattern, or figure is tested against a hypothesis that there is no relationship or pattern among the variables being tested

Null hypothesis significance testing.

The error you make when you do not infer a relationship exists in the larger population when it actually does exist; in other words, a false negative conclusion.

The error made if one infers that a relationship exists in a larger population when it does not really exist; in other words, a false positive error.

A measure of accuracy of sample statistics computed using the standard deviation of the sampling distribution.

The hypothesis that there is no relationship between the variables in question.

The probability that the sample statistics we observe holds true for the larger population.

A measure of statistical significance used in crosstabulation to determine the generalizability of results.

A range of estimates into which it is highly probable that an unknown population parameter falls.

A suggestion of how far away from the actual population parameter a sample statistic is likely to be.

Social Data Analysis Copyright © 2021 by Mikaila Mariel Lemonik Arthur is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Hypothesis tests

• Author information
• Article notes
• Copyright and License information

Accepted 2019 Mar 28; Issue date 2019 Jul.

Key points.

Hypothesis tests are used to assess whether a difference between two samples represents a real difference between the populations from which the samples were taken.

A null hypothesis of ‘no difference’ is taken as a starting point, and we calculate the probability that both sets of data came from the same population. This probability is expressed as a p -value.

When the null hypothesis is false, p- values tend to be small. When the null hypothesis is true, any p- value is equally likely.

Learning objectives.

By reading this article, you should be able to:

Explain why hypothesis testing is used.

Use a table to determine which hypothesis test should be used for a particular situation.

Interpret a p- value.

A hypothesis test is a procedure used in statistics to assess whether a particular viewpoint is likely to be true. They follow a strict protocol, and they generate a ‘ p- value’, on the basis of which a decision is made about the truth of the hypothesis under investigation. All of the routine statistical ‘tests’ used in research— t- tests, χ 2 tests, Mann–Whitney tests, etc.—are all hypothesis tests, and in spite of their differences they are all used in essentially the same way. But why do we use them at all?

Comparing the heights of two individuals is easy: we can measure their height in a standardised way and compare them. When we want to compare the heights of two small well-defined groups (for example two groups of children), we need to use a summary statistic that we can calculate for each group. Such summaries (means, medians, etc.) form the basis of descriptive statistics, and are well described elsewhere. 1 However, a problem arises when we try to compare very large groups or populations: it may be impractical or even impossible to take a measurement from everyone in the population, and by the time you do so, the population itself will have changed. A similar problem arises when we try to describe the effects of drugs—for example by how much on average does a particular vasopressor increase MAP?

To solve this problem, we use random samples to estimate values for populations. By convention, the values we calculate from samples are referred to as statistics and denoted by Latin letters ( x ¯ for sample mean; SD for sample standard deviation) while the unknown population values are called parameters , and denoted by Greek letters (μ for population mean, σ for population standard deviation).

Inferential statistics describes the methods we use to estimate population parameters from random samples; how we can quantify the level of inaccuracy in a sample statistic; and how we can go on to use these estimates to compare populations.

Sampling error

There are many reasons why a sample may give an inaccurate picture of the population it represents: it may be biased, it may not be big enough, and it may not be truly random. However, even if we have been careful to avoid these pitfalls, there is an inherent difference between the sample and the population at large. To illustrate this, let us imagine that the actual average height of males in London is 174 cm. If I were to sample 100 male Londoners and take a mean of their heights, I would be very unlikely to get exactly 174 cm. Furthermore, if somebody else were to perform the same exercise, it would be unlikely that they would get the same answer as I did. The sample mean is different each time it is taken, and the way it differs from the actual mean of the population is described by the standard error of the mean (standard error, or SEM ). The standard error is larger if there is a lot of variation in the population, and becomes smaller as the sample size increases. It is calculated thus:

where SD is the sample standard deviation, and n is the sample size.

As errors are normally distributed, we can use this to estimate a 95% confidence interval on our sample mean as follows:

We can interpret this as meaning ‘We are 95% confident that the actual mean is within this range.’

Some confusion arises at this point between the SD and the standard error. The SD is a measure of variation in the sample. The range x ¯ ± ( 1.96 × SD ) will normally contain 95% of all your data. It can be used to illustrate the spread of the data and shows what values are likely. In contrast, standard error tells you about the precision of the mean and is used to calculate confidence intervals.

One straightforward way to compare two samples is to use confidence intervals. If we calculate the mean height of two groups and find that the 95% confidence intervals do not overlap, this can be taken as evidence of a difference between the two means. This method of statistical inference is reasonably intuitive and can be used in many situations. 2 Many journals, however, prefer to report inferential statistics using p -values.

Inference testing using a null hypothesis

In 1925, the British statistician R.A. Fisher described a technique for comparing groups using a null hypothesis , a method which has dominated statistical comparison ever since. The technique itself is rather straightforward, but often gets lost in the mechanics of how it is done. To illustrate, imagine we want to compare the HR of two different groups of people. We take a random sample from each group, which we call our data. Then:

Assume that both samples came from the same group. This is our ‘null hypothesis’.

Calculate the probability that an experiment would give us these data, assuming that the null hypothesis is true. We express this probability as a p- value, a number between 0 and 1, where 0 is ‘impossible’ and 1 is ‘certain’.

If the probability of the data is low, we reject the null hypothesis and conclude that there must be a difference between the two groups.

Formally, we can define a p- value as ‘the probability of finding the observed result or a more extreme result, if the null hypothesis were true.’ Standard practice is to set a cut-off at p <0.05 (this cut-off is termed the alpha value). If the null hypothesis were true, a result such as this would only occur 5% of the time or less; this in turn would indicate that the null hypothesis itself is unlikely. Fisher described the process as follows: ‘Set a low standard of significance at the 5 per cent point, and ignore entirely all results which fail to reach this level. A scientific fact should be regarded as experimentally established only if a properly designed experiment rarely fails to give this level of significance.’ 3 This probably remains the most succinct description of the procedure.

A question which often arises at this point is ‘Why do we use a null hypothesis?’ The simple answer is that it is easy: we can readily describe what we would expect of our data under a null hypothesis, we know how data would behave, and we can readily work out the probability of getting the result that we did. It therefore makes a very simple starting point for our probability assessment. All probabilities require a set of starting conditions, in much the same way that measuring the distance to London needs a starting point. The null hypothesis can be thought of as an easy place to put the start of your ruler.

If a null hypothesis is rejected, an alternate hypothesis must be adopted in its place. The null and alternate hypotheses must be mutually exclusive, but must also between them describe all situations. If a null hypothesis is ‘no difference exists’ then the alternate should be simply ‘a difference exists’.

Hypothesis testing in practice

The components of a hypothesis test can be readily described using the acronym GOST: identify the Groups you wish to compare; define the Outcome to be measured; collect and Summarise the data; then evaluate the likelihood of the null hypothesis, using a Test statistic .

When considering groups, think first about how many. Is there just one group being compared against an audit standard, or are you comparing one group with another? Some studies may wish to compare more than two groups. Another situation may involve a single group measured at different points in time, for example before or after a particular treatment. In this situation each participant is compared with themselves, and this is often referred to as a ‘paired’ or a ‘repeated measures’ design. It is possible to combine these types of groups—for example a researcher may measure arterial BP on a number of different occasions in five different groups of patients. Such studies can be difficult, both to analyse and interpret.

In other studies we may want to see how a continuous variable (such as age or height) affects the outcomes. These techniques involve regression analysis, and are beyond the scope of this article.

The outcome measures are the data being collected. This may be a continuous measure, such as temperature or BMI, or it may be a categorical measure, such as ASA status or surgical specialty. Often, inexperienced researchers will strive to collect lots of outcome measures in an attempt to find something that differs between the groups of interest; if this is done, a ‘primary outcome measure’ should be identified before the research begins. In addition, the results of any hypothesis tests will need to be corrected for multiple measures.

The summary and the test statistic will be defined by the type of data that have been collected. The test statistic is calculated then transformed into a p- value using tables or software. It is worth looking at two common tests in a little more detail: the χ 2 test, and the t -test.

Categorical data: the χ 2 test

The χ 2 test of independence is a test for comparing categorical outcomes in two or more groups. For example, a number of trials have compared surgical site infections in patients who have been given different concentrations of oxygen perioperatively. In the PROXI trial, 4 685 patients received oxygen 80%, and 701 patients received oxygen 30%. In the 80% group there were 131 infections, while in the 30% group there were 141 infections. In this study, the groups were oxygen 80% and oxygen 30%, and the outcome measure was the presence of a surgical site infection.

The summary is a table ( Table 1 ), and the hypothesis test compares this table (the ‘observed’ table) with the table that would be expected if the proportion of infections in each group was the same (the ‘expected’ table). The test statistic is χ 2 , from which a p- value is calculated. In this instance the p -value is 0.64, which means that results like this would occur 64% of the time if the null hypothesis were true. We thus have no evidence to reject the null hypothesis; the observed difference probably results from sampling variation rather than from an inherent difference between the two groups.

Summary of the results of the PROXI trial. Figures are numbers of patients.

Continuous data: the t- test

The t- test is a statistical method for comparing means, and is one of the most widely used hypothesis tests. Imagine a study where we try to see if there is a difference in the onset time of a new neuromuscular blocking agent compared with suxamethonium. We could enlist 100 volunteers, give them a general anaesthetic, and randomise 50 of them to receive the new drug and 50 of them to receive suxamethonium. We then time how long it takes (in seconds) to have ideal intubation conditions, as measured by a quantitative nerve stimulator. Our data are therefore a list of times. In this case, the groups are ‘new drug’ and suxamethonium, and the outcome is time, measured in seconds. This can be summarised by using means; the hypothesis test will compare the means of the two groups, using a p- value calculated from a ‘ t statistic’. Hopefully it is becoming obvious at this point that the test statistic is usually identified by a letter, and this letter is often cited in the name of the test.

The t -test comes in a number of guises, depending on the comparison being made. A single sample can be compared with a standard (Is the BMI of school leavers in this town different from the national average?); two samples can be compared with each other, as in the example above; or the same study subjects can be measured at two different times. The latter case is referred to as a paired t- test, because each participant provides a pair of measurements—such as in a pre- or postintervention study.

A large number of methods for testing hypotheses exist; the commonest ones and their uses are described in Table 2 . In each case, the test can be described by detailing the groups being compared ( Table 2 , columns) the outcome measures (rows), the summary, and the test statistic. The decision to use a particular test or method should be made during the planning stages of a trial or experiment. At this stage, an estimate needs to be made of how many test subjects will be needed. Such calculations are described in detail elsewhere. 5

The principle types of hypothesis test. Tests comparing more than two samples can indicate that one group differs from the others, but will not identify which. Subsequent ‘post hoc’ testing is required if a difference is found.

Controversies surrounding hypothesis testing

Although hypothesis tests have been the basis of modern science since the middle of the 20th century, they have been plagued by misconceptions from the outset; this has led to what has been described as a crisis in science in the last few years: some journals have gone so far as to ban p -value s outright. 6 This is not because of any flaw in the concept of a p -value, but because of a lack of understanding of what they mean.

Possibly the most pervasive misunderstanding is the belief that the p- value is the chance that the null hypothesis is true, or that the p- value represents the frequency with which you will be wrong if you reject the null hypothesis (i.e. claim to have found a difference). This interpretation has frequently made it into the literature, and is a very easy trap to fall into when discussing hypothesis tests. To avoid this, it is important to remember that the p- value is telling us something about our sample , not about the null hypothesis. Put in simple terms, we would like to know the probability that the null hypothesis is true, given our data. The p- value tells us the probability of getting these data if the null hypothesis were true, which is not the same thing. This fallacy is referred to as ‘flipping the conditional’; the probability of an outcome under certain conditions is not the same as the probability of those conditions given that the outcome has happened.

A useful example is to imagine a magic trick in which you select a card from a normal deck of 52 cards, and the performer reveals your chosen card in a surprising manner. If the performer were relying purely on chance, this would only happen on average once in every 52 attempts. On the basis of this, we conclude that it is unlikely that the magician is simply relying on chance. Although simple, we have just performed an entire hypothesis test. We have declared a null hypothesis (the performer was relying on chance); we have even calculated a p -value (1 in 52, ≈0.02); and on the basis of this low p- value we have rejected our null hypothesis. We would, however, be wrong to suggest that there is a probability of 0.02 that the performer is relying on chance—that is not what our figure of 0.02 is telling us.

To explore this further we can create two populations, and watch what happens when we use simulation to take repeated samples to compare these populations. Computers allow us to do this repeatedly, and to see what p- value s are generated (see Supplementary online material). 7 Fig 1 illustrates the results of 100,000 simulated t -tests, generated in two set of circumstances. In Fig 1 a , we have a situation in which there is a difference between the two populations. The p- value s cluster below the 0.05 cut-off, although there is a small proportion with p >0.05. Interestingly, the proportion of comparisons where p <0.05 is 0.8 or 80%, which is the power of the study (the sample size was specifically calculated to give a power of 80%).

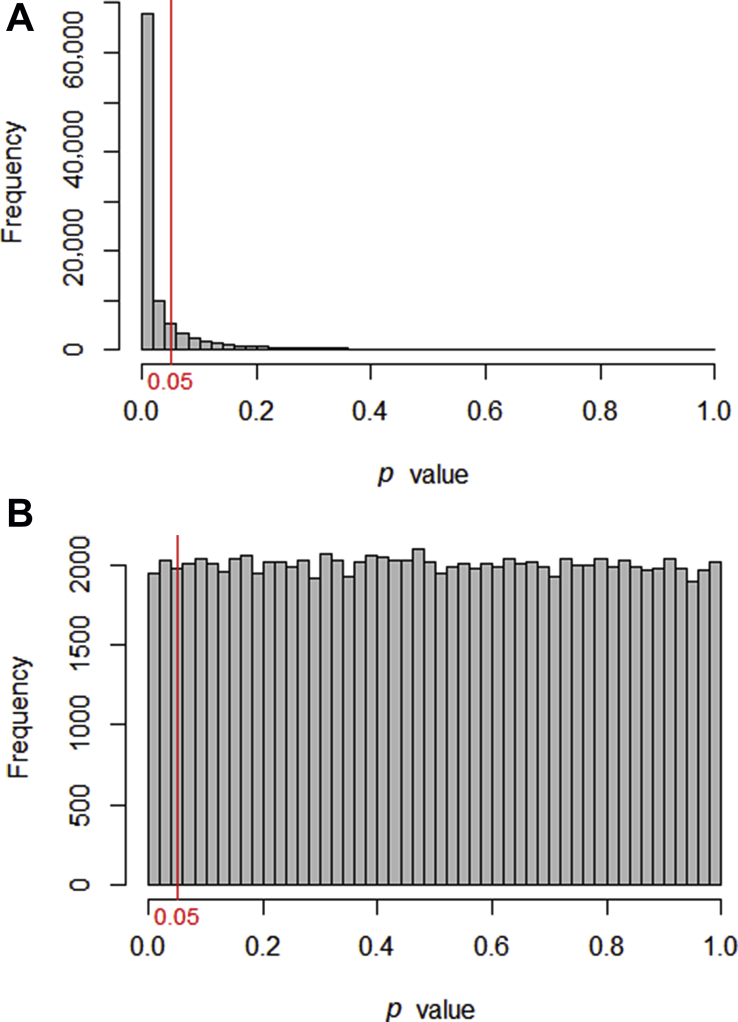
The p- value s generated when 100,000 t -tests are used to compare two samples taken from defined populations. ( a ) The populations have a difference and the p- value s are mostly significant. ( b ) The samples were taken from the same population (i.e. the null hypothesis is true) and the p- value s are distributed uniformly.

Figure 1 b depicts the situation where repeated samples are taken from the same parent population (i.e. the null hypothesis is true). Somewhat surprisingly, all p- value s occur with equal frequency, with p <0.05 occurring exactly 5% of the time. Thus, when the null hypothesis is true, a type I error will occur with a frequency equal to the alpha significance cut-off.

Figure 1 highlights the underlying problem: when presented with a p -value <0.05, is it possible with no further information, to determine whether you are looking at something from Fig 1 a or Fig 1 b ?

Finally, it cannot be stressed enough that although hypothesis testing identifies whether or not a difference is likely, it is up to us as clinicians to decide whether or not a statistically significant difference is also significant clinically.

Hypothesis testing: what next?

As mentioned above, some have suggested moving away from p -values, but it is not entirely clear what we should use instead. Some sources have advocated focussing more on effect size; however, without a measure of significance we have merely returned to our original problem: how do we know that our difference is not just a result of sampling variation?

One solution is to use Bayesian statistics. Up until very recently, these techniques have been considered both too difficult and not sufficiently rigorous. However, recent advances in computing have led to the development of Bayesian equivalents of a number of standard hypothesis tests. 8 These generate a ‘Bayes Factor’ (BF), which tells us how more (or less) likely the alternative hypothesis is after our experiment. A BF of 1.0 indicates that the likelihood of the alternate hypothesis has not changed. A BF of 10 indicates that the alternate hypothesis is 10 times more likely than we originally thought. A number of classifications for BF exist; greater than 10 can be considered ‘strong evidence’, while BF greater than 100 can be classed as ‘decisive’.

Figures such as the BF can be quoted in conjunction with the traditional p- value, but it remains to be seen whether they will become mainstream.

Declaration of interest

The author declares that they have no conflict of interest.

The associated MCQs (to support CME/CPD activity) will be accessible at www.bjaed.org/cme/home by subscribers to BJA Education .

Jason Walker FRCA FRSS BSc (Hons) Math Stat is a consultant anaesthetist at Ysbyty Gwynedd Hospital, Bangor, Wales, and an honorary senior lecturer at Bangor University. He is vice chair of his local research ethics committee, and an examiner for the Primary FRCA.

Matrix codes: 1A03, 2A04, 3J03

Supplementary data to this article can be found online at https://doi.org/10.1016/j.bjae.2019.03.006 .

Supplementary material

The following is the Supplementary data to this article:

• 1. McCluskey A., Lalkhen A.G. Statistics II: central tendency and spread of data. CEACCP. 2007;7:127–130. [ Google Scholar ]
• 2. Altman D.G., Machin D., Bryant T.N., Gardner M.J. 2nd Edn. BMJ Books; London: 2000. Statistics with confidence. [ Google Scholar ]
• 3. Fisher R.A. The arrangement of field experiments. J Min Agric Gr Br. 1926;33:503–513. [ Google Scholar ]
• 4. Meyhoff C.S., Wetterslev J., Jorgensen L.N. Effect of high perioperative oxygen fraction on surgical site infection and pulmonary complications after abdominal surgery: the PROXI randomized clinical trial. JAMA. 2009;302:1543–1550. doi: 10.1001/jama.2009.1452. [ DOI ] [ PubMed ] [ Google Scholar ]
• 5. Columb M.O., Atkinson M.S. Statistical analysis: sample size and power estimations. BJA Educ. 2016;16:159–161. [ Google Scholar ]
• 6. Trafimow D., Marks M. Editorial. Basic Appl Soc Psych. 2015;37:1–2. [ Google Scholar ]
• 7. Colquhoun D. An investigation of the false discovery rate and the misinterpretation of p-values. R Soc Open Sci. 2014;1:140216. doi: 10.1098/rsos.140216. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 8. Ly A., Verhagen J., Wagenmakers E. Harold Jeffreys’s default Bayes factor hypothesis tests: explanation, extension, and application in psychology. J Math Psychol. 2016;72:19–32. [ Google Scholar ]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

• View on publisher site
• PDF (344.3 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections

Hypothesis Testing

Measuring the consistency between a model and data

C lassical statistics features two primary methods for using a sample of data to make an inference about a more general process. The first is the confidence interval, which expresses the uncertainty in an estimate of a population parameter. The second classical method of generalization is the hypothesis test.

The hypothesis test takes a more active approach to reasoning: it posits a specific explanation for how the data could be generated, then evaluates whether or not the observed data is consistent with that model. The hypothesis test is one of the most common statistical tools in the social and natural sciences, but the reasoning involved can be counter-intuitive. Let’s introduce the logic of a hypothesis test by looking at another criminal case that drew statisticians into the mix.

Example: The United States vs Kristen Gilbert

In 1989, fresh out of nursing school, Kristen Gilbert got a job at the VA Medical Center in Northampton, Massachusetts, not far from where she grew up 1 . Within a few years, she became admired for her skill and competence.

Gilbert’s skill was on display whenever a “code blue” alarm was sounded. This alarm indicates that a patient has gone into cardiac arrest and must be addressed quickly by administering a shot of epinephrine to restart the heart. Gilbert developed for a reputation for her steady hand in these crises.

By the mid-1990s, however, the other nurses started to grow suspicious. There seemed to be a few too many code blues, and a few too many deaths, during Gilbert’s shifts. The staff brought their concerns to the VA administration, who brought in a statistician to evaluate the data.

The data that the VA provided to the statistician contained the number of deaths at the medical center over the previous 10 years, broken out by the three shifts of the days: night, daytime, and evening. As part of the process of exploratory data analysis, the statistician constructed a plot.

This visualization reveals several striking trends. Between 1990 and 1995, there were dramatically more deaths than the years before and after that interval. Within that time span, it was the evening shift that had most of the deaths. The exception is 1990, when the night and daytime shifts had the most deaths.

So when was Gilbert working? She began working in this part of the hospital in March 1990 and stopped working in February 1996. Her shifts throughout that time span? The evening shifts. The one exception was 1990, when she was assigned to work the night shift.

This evidence is compelling in establishing an association between Gilbert and the increase in deaths. When the district attorney brought a case against Gilbert in court, this was the first line of evidence they provided. In a trial, however, there is a high burden of proof.

Could there be an alternative explanation for the trend found in this data?

The role of random chance

Suppose for a moment that the occurrence of deaths at the hospital had nothing to do with Gilbert being on shift. In that case we would expect that the proportion of shifts with a death would be fairly similar when comparing shifts where Gilbert was working and shifts where she was not. But we wouldn’t expect those proportions to be exactly equal. It’s reasonable to think that a slightly higher proportion of Gilbert’s shifts could have had a death just due to random chance, not due to anything malicious on her part.

So just how different were these proportions in the data? The plot above shows data from 1,641 individual shifts, on which three different variables were recorded: the shift number, whether or not there was a death on the shift, and whether or not Gilbert was working that shift.

Here are the first 10 observations.

Using this data frame, we can calculate the sample proportion of shifts where Gilbert was working (257) that had a death (40) and compare them to the sample proportion of shifts where Gilbert was not working (1384) that had a death (34).

\[ \hat{p}_{gilbert} - \hat{p}_{no\_gilbert} = \frac{40}{257} - \frac{34}{1384} = .155 - .024 = .131 \]

A note on notation: it’s common to use \(\hat{p}\) (“p hat”) to indicate that a proportion has been computed from a sample of data.

A difference of .131 seems dramatic, but is that within the bounds of what we might expect just due to chance? One way to address this question is to phrase it as: if in fact the probability of a death on a given shift is independent of whether or not Gilbert is on the shift, what values would we expect for the difference in observed proportions?

We can answer this question by using simulation. To a simulate a world in which deaths are independent of Gilbert, we can

• Shuffle (or permute) the values in the death variable in the data frame to break the link between that variable and the staff variable.
• Calculate the resulting difference in proportion of deaths in each group.

The rationale for shuffling values in one of the columns is that if in fact those two columns are independent of one another, then it was just random chance that led to a value of one variable landing in the same row as the value of the other variable. It could just as well have been a different pairing. Shuffling captures another example of the arbitrary pairings that we could have observed if the two variables were independent of one another 2 .

By repeating steps 1 and 2 many many times, we can build up the full distribution of the values that this difference in proportions could take.

As expected, in a world where these two variables are independent of one another, we would expect a difference in proportions around zero. Sometimes, however, that statistic might reach values of +/- .01 or .02 or rarely .03. In the 500 simulated statistics shown above, however, none of them reached beyond +/- .06.

So if that’s the range of statistics we would expect in a world where random chance is the only mechanism driving the difference in proportions, how does it compare to the world that we actually observed? The statistic that we observed in the data was .131, more than twice the value of the most extreme statistic observed above.

To put that into perspective, we can plot the observed statistic as a vertical line on the same plot.

The method used above shows that the chance of observing a difference of .131 is incredibly unlikely if in fact deaths were independent of Gilbert being on shift. On this point, the statisticians on the case agreed that they could rule out random chance as an explanation for this difference. Something else must have been happening.

Elements of a Hypothesis Test

The logic used by the statisticians in the Gilbert case is an example of a hypothesis test. There are a few key components common to every hypothesis test, so we’ll lay them out one-by-one.

A hypothesis test begins with the assertion of a null hypothesis.

It is common for the null hypothesis to be that nothing interesting is happening or that it is business as usual, a hypothesis that statisticians try to refute with data. In Gilbert case, this could be described as “The occurrence of a death is independence of the presence of Gilbert” or “The probability of death is the same whether or not Gilbert is on shift” or “The difference in the probability of death is zero, when comparing shifts where Gilbert is present to shifts where Gilbert is not present”. Importantly, the null model describes a possible state of the world, therefore the latter two versions are framed in terms of parameters ( \(p\) for proportions) instead of observed statistics ( \(\hat{p}\) ).

The hypothesis that something indeed is going on is usually framed as the alternative hypothesis.

In the Gilbert case, the corresponding alternative hypothesis is that there is “The occurrence of a death is dependent on the presence of Gilbert” or “The probability of death is different whether or not Gilbert is on shift” or “The difference in the probability of death is non-zero , when comparing shifts where Gilbert is present to shifts where Gilbert is not present”

In order to determine whether the observed data is consistent with the null hypothesis, it is necessary to compress the data down into a single statistic.

In Gilbert’s case, a difference in two proportions, \(\hat{p}_1 - \hat{p}_2\) is a natural test statistic and the observed test statistic was .131.

It’s not enough, though, to just compute the observed statistic. We need to know how likely this statistic would be in a world where the null hypothesis is true. This probability is captured in the notion of a p-value.

If the p-value is high, then the data is consistent with the null hypothesis. If the p-value is very low, however, there the statistic that was observed would be very unlikely in a world where the null hypothesis was true. As a consequence, the null hypothesis can be rejected as reasonable model for the data.

The p-value can be estimated using the proportion of statistics from the simulated null distribution that are as or more extreme than the observed statistic. In the simulation for the Gilbert case, there were 0 statistics greater than .131, so the estimated p-value is zero.

What a p-value is not

The p-value has been called the most used as well as the most abused tool in statistics. Here are three common misinterpretations to be wary of.

The p-value is the probability that the null hypothesis is true (FALSE!)

This is one of the most common confusions about p-values. Graphically, a p-value corresponds to the area in the tail of the null distribution that is more extreme than the observed test statistic. That null distribution can only be created if you assume that the null hypothesis is true. The p-value is fundamentally a conditional probability of observing the statistic (or more extreme) given the null hypothesis is true. It is flawed reasoning to start with an assumption that the null hypothesis is true and arrive at a probability of that same assumption.

A very high p-value suggests that the null hypothesis is true (FALSE!)

This interpretation is related to the first one but can lead to particularly wrongheaded decisions. One way to keep your interpretation of a p-value straight is to recall the distinction made in the US court system. A trial proceeds under the assumption that the defendant is innocent. The prosecution presents evidence of guilt. If the evidence is convincing the jury will render a verdict of “guilty”. If the evidence is not-convincing (that is, the p-value is high) then the jury will render a verdict of “not guilty” - not a verdict of “innocent”.

Imagine a setting where the prosecution has presented no evidence at all. That by no means indicates that the defendant is innocent, just that there was insufficient evidence to establish guilt.

The p-value is the probability of the data (FALSE!)

This statement has a semblance of truth to it but is missing an important qualifier. The probability is calculated based on the null distribution, which requires the assumption that the null hypothesis is true. It’s also not quite specific enough. Most often p-values are calculated as probabilities of test statistics, not probabilities of the full data sets.

Another more basic check on your understanding of a p-value: a p-value is a (conditional) probability, therefore it must between a number between 0 and 1. If you ever find yourself computing a p-value of -6 or 3.2, be sure to pause and revisit your calculations!

One test, many variations

The hypothesis testing framework laid out above is far more general than just this particular example from the case of Kristen Gilbert where we computed a difference in proportions and used shuffling (aka permutation) to build the null distribution. Below are just a few different research questions that could be addressed using a hypothesis test.

Pollsters have surveyed a sample of 200 voters ahead of an election to assess their relative support for the Republican and Democratic candidate. The observed difference in those proportions is .02. Is this consistent with the notion of evenly split support for the two candidates, or is one decidedly in the lead?

Brewers have tapped 7 barrels of beer and measured the average level of a compound related to the acidity of the beer as 610 parts per million. The acceptable level for this compound is 500 parts per million. Is this average of 610 consistent with the notion that the average of the whole batch of beer (many hundreds of barrels) is at the acceptable level of this compound?

A random sample of 40 users of a food delivery app were randomly assigned two different versions of a menu where they entered the amount of their tip: one with the tip amount in ascending order, the other in descending order. The average tip amount of those with the menu in ascending order was found to be $3.87 while the average tip of the users in the descending order group was $3.96. Could this difference in averages be explained by chance?

Although the contexts of these problems are very different, as are the types of statistics they’ve calculated, they can still be characterized as a hypothesis test by asking the following questions:

What is the null hypothesis used by the researchers?

What is the value of the observed test statistic?

How did researchers approximate the null distribution?

What was the p-value, what does it tell us and what does it not tell us?

In classical statistics there are two primary tools for assessing the role that random variability plays in the data that you have observed. The first is the confidence interval, which quantifies the amount of uncertainty in a point estimate due to the variability inherent in drawing a small random sample from a population. The second is the hypothesis test, which postings a specific model by which the data could be generated, then assesses the degree to which the observed data is consistent with that model.

The hypothesis test begins with the assertion of a null hypothesis that describes a chance mechanism for generating data. A test statistic is then selected that corresponds to that null hypothesis. From there, the sampling distribution of that statistic under the null hypothesis is approximated through a computational method (such as using permutation, as shown here) or one rooted in probability theory (such as the Central Limit Theorem). The final result of the hypothesis test procedure is the p-value, which is approximated as the proportion of the null distribution that is as or more extreme than the observed test statistic. The p-value measures the consistency between the null hypothesis and the observed test statistic and should be interpreted carefully.

A postscript on the case of Kristen Gilbert. Although the hypothesis test ruled out random chance as the reason for the spike in deaths under her watch, it didn’t rule out other potential causes for that spike. It’s possible, after all, that the nightshifts that Gilbert was working happen to be the time of day when cardiac arrests are more common. For this reason, the statistical evidence was never presented to the jury, but the jury nonetheless found her guilty based on other evidence presented in the trial.

The Ideas in Code

A hypothesis test using permutation can be implemented by introducing one new step into the process used for calculating a bootstrap interval. The key distinction is that in a hypothesis test the researchers puts forth a model for how the data could be generated. That is the role of hypothesize() .

hypothesize()

A function to place before generate() in an infer pipeline where you can specify a null model under which to generate data. The one necessary argument is

• null : the null hypothesis. Options include "independence" and "point" .

The following example implements a permutation test under the null hypothesis that there is no relationship between the body mass of penguins and their

• The output is the original data frame with new information appended to describe what the null hypothesis is for this data set.
• There are other forms of hypothesis tests that you will see involving a "point" null hypothesis. Those require adding additional arguments to hypothesize() .

Calculating an observed statistic

Let’s say for this example you select as your test statistic a difference in means, \(\bar{x}_{female} - \bar{x}_{male}\) . While you can use tools you know - group_by() and summarize() to calculate this statistic, you can also recycle much of the code that you’ll use to build the null distribution with infer .

Calculating the null distribution

To generate a null distribution of the kind of differences in means that you’d observe in a world where body mass had nothing to do with sex, just add the hypothesis with hypothesize() and the generation mechanism with generate() .

• The output data frame has reps rows and 2 columns: one indicating the replicate and the other with the statistic (a difference in means).

visualize()

Once you have a collection of test statistics under the null hypothesis saved as null , it can be useful to visualize that approximation of the null distribution. For that, use the function visualize() .

• visualize() expects a data frame of statistics.
• It is a short cut to creating a particular type of ggplot, so like any ggplot, you can add layers to it with + +.
• shade_p_value() is a function you can add to shade the part of the null distribution that corresponds to the p-value. The first argument is the observed statistic, which we’ve recorded as 100 here to see the behavior of the function. direction is an argument where you specify if you would like to shade values "less than" or "more than" the observed value, or "both" for a two-tailed p-value.

This case study appears in Statistics in the Courtroom: United States v. Kristen Gilbert by Cobb and Gelbach, published in Statistics: A Guide to the Unknown by Peck et. al. ↩︎

The technical notion that motivates the use of shuffling is a slightly more general notion than independence called exchangability. The distinction between these two related concepts is a topic in a course in probability. ↩︎

Quantitative Research Methods

• Introduction
• Descriptive and Inferential Statistics
• Hypothesis Testing
• Regression and Correlation
• Time Series
• Meta-Analysis
• Mixed Methods
• Additional Resources
• Get Research Help

Hypothesis Tests

A hypothesis test is exactly what it sounds like: You make a hypothesis about the parameters of a population, and the test determines whether your hypothesis is consistent with your sample data.

• Hypothesis Testing Penn State University tutorial
• Hypothesis Testing Wolfram MathWorld overview
• Hypothesis Testing Minitab Blog entry
• List of Statistical Tests A list of commonly used hypothesis tests and the circumstances under which they're used.

The p-value of a hypothesis test is the probability that your sample data would have occurred if you hypothesis were not correct. Traditionally, researchers have used a p-value of 0.05 (a 5% probability that your sample data would have occurred if your hypothesis was wrong) as the threshold for declaring that a hypothesis is true. But there is a long history of debate and controversy over p-values and significance levels.

Nonparametric Tests

Many of the most commonly used hypothesis tests rely on assumptions about your sample data—for instance, that it is continuous, and that its parameters follow a Normal distribution. Nonparametric hypothesis tests don't make any assumptions about the distribution of the data, and many can be used on categorical data.

• Nonparametric Tests at Boston University A lesson covering four common nonparametric tests.
• Nonparametric Tests at Penn State Tutorial covering the theory behind nonparametric tests as well as several commonly used tests.
• << Previous: Descriptive and Inferential Statistics
• Next: Regression and Correlation >>
• Last Updated: Aug 16, 2024 1:12 PM
• URL: https://guides.library.duq.edu/quant-methods