Quasi-Experimental Design: Definition, Types, Examples
Appinio Research · 19.12.2023 · 37min read

Ever wondered how researchers uncover cause-and-effect relationships in the real world, where controlled experiments are often elusive? Quasi-experimental design holds the key. In this guide, we'll unravel the intricacies of quasi-experimental design, shedding light on its definition, purpose, and applications across various domains. Whether you're a student, a professional, or simply curious about the methods behind meaningful research, join us as we delve into the world of quasi-experimental design, making complex concepts sound simple and embarking on a journey of knowledge and discovery.

What is Quasi-Experimental Design?
Quasi-experimental design is a research methodology used to study the effects of independent variables on dependent variables when full experimental control is not possible or ethical. It falls between controlled experiments, where variables are tightly controlled, and purely observational studies, where researchers have little control over variables. Quasi-experimental design mimics some aspects of experimental research but lacks randomization.
The primary purpose of quasi-experimental design is to investigate cause-and-effect relationships between variables in real-world settings. Researchers use this approach to answer research questions, test hypotheses, and explore the impact of interventions or treatments when they cannot employ traditional experimental methods. Quasi-experimental studies aim to maximize internal validity and make meaningful inferences while acknowledging practical constraints and ethical considerations.
Quasi-Experimental vs. Experimental Design
It's essential to understand the distinctions between Quasi-Experimental and Experimental Design to appreciate the unique characteristics of each approach:
- Randomization: In Experimental Design, random assignment of participants to groups is a defining feature. Quasi-experimental design, on the other hand, lacks randomization due to practical constraints or ethical considerations.
- Control Groups : Experimental Design typically includes control groups that are subjected to no treatment or a placebo. The quasi-experimental design may have comparison groups but lacks the same level of control.
- Manipulation of IV: Experimental Design involves the intentional manipulation of the independent variable. Quasi-experimental design often deals with naturally occurring independent variables.
- Causal Inference: Experimental Design allows for stronger causal inferences due to randomization and control. Quasi-experimental design permits causal inferences but with some limitations.
When to Use Quasi-Experimental Design?
A quasi-experimental design is particularly valuable in several situations:
- Ethical Constraints: When manipulating the independent variable is ethically unacceptable or impractical, quasi-experimental design offers an alternative to studying naturally occurring variables.
- Real-World Settings: When researchers want to study phenomena in real-world contexts, quasi-experimental design allows them to do so without artificial laboratory settings.
- Limited Resources: In cases where resources are limited and conducting a controlled experiment is cost-prohibitive, quasi-experimental design can provide valuable insights.
- Policy and Program Evaluation: Quasi-experimental design is commonly used in evaluating the effectiveness of policies, interventions, or programs that cannot be randomly assigned to participants.
Importance of Quasi-Experimental Design in Research
Quasi-experimental design plays a vital role in research for several reasons:
- Addressing Real-World Complexities: It allows researchers to tackle complex real-world issues where controlled experiments are not feasible. This bridges the gap between controlled experiments and purely observational studies.
- Ethical Research: It provides an honest approach when manipulating variables or assigning treatments could harm participants or violate ethical standards.
- Policy and Practice Implications: Quasi-experimental studies generate findings with direct applications in policy-making and practical solutions in fields such as education, healthcare, and social sciences.
- Enhanced External Validity: Findings from Quasi-Experimental research often have high external validity, making them more applicable to broader populations and contexts.
By embracing the challenges and opportunities of quasi-experimental design, researchers can contribute valuable insights to their respective fields and drive positive changes in the real world.
Key Concepts in Quasi-Experimental Design
In quasi-experimental design, it's essential to grasp the fundamental concepts underpinning this research methodology. Let's explore these key concepts in detail.
Independent Variable
The independent variable (IV) is the factor you aim to study or manipulate in your research. Unlike controlled experiments, where you can directly manipulate the IV, quasi-experimental design often deals with naturally occurring variables. For example, if you're investigating the impact of a new teaching method on student performance, the teaching method is your independent variable.
Dependent Variable
The dependent variable (DV) is the outcome or response you measure to assess the effects of changes in the independent variable. Continuing with the teaching method example, the dependent variable would be the students' academic performance, typically measured using test scores, grades, or other relevant metrics.
Control Groups vs. Comparison Groups
While quasi-experimental design lacks the luxury of randomly assigning participants to control and experimental groups, you can still establish comparison groups to make meaningful inferences. Control groups consist of individuals who do not receive the treatment, while comparison groups are exposed to different levels or variations of the treatment. These groups help researchers gauge the effect of the independent variable.
Pre-Test and Post-Test Measures
In quasi-experimental design, it's common practice to collect data both before and after implementing the independent variable. The initial data (pre-test) serves as a baseline, allowing you to measure changes over time (post-test). This approach helps assess the impact of the independent variable more accurately. For instance, if you're studying the effectiveness of a new drug, you'd measure patients' health before administering the drug (pre-test) and afterward (post-test).
Threats to Internal Validity
Internal validity is crucial for establishing a cause-and-effect relationship between the independent and dependent variables. However, in a quasi-experimental design, several threats can compromise internal validity. These threats include:
- Selection Bias : When non-randomized groups differ systematically in ways that affect the study's outcome.
- History Effects: External events or changes over time that influence the results.
- Maturation Effects: Natural changes or developments that occur within participants during the study.
- Regression to the Mean: The tendency for extreme scores on a variable to move closer to the mean upon retesting.
- Attrition and Mortality: The loss of participants over time, potentially skewing the results.
- Testing Effects: The mere act of testing or assessing participants can impact their subsequent performance.
Understanding these threats is essential for designing and conducting Quasi-Experimental studies that yield valid and reliable results.
Randomization and Non-Randomization
In traditional experimental designs, randomization is a powerful tool for ensuring that groups are equivalent at the outset of a study. However, quasi-experimental design often involves non-randomization due to the nature of the research. This means that participants are not randomly assigned to treatment and control groups. Instead, researchers must employ various techniques to minimize biases and ensure that the groups are as similar as possible.
For example, if you are conducting a study on the effects of a new teaching method in a real classroom setting, you cannot randomly assign students to the treatment and control groups. Instead, you might use statistical methods to match students based on relevant characteristics such as prior academic performance or socioeconomic status. This matching process helps control for potential confounding variables, increasing the validity of your study.
Types of Quasi-Experimental Designs
In quasi-experimental design, researchers employ various approaches to investigate causal relationships and study the effects of independent variables when complete experimental control is challenging. Let's explore these types of quasi-experimental designs.
One-Group Posttest-Only Design
The One-Group Posttest-Only Design is one of the simplest forms of quasi-experimental design. In this design, a single group is exposed to the independent variable, and data is collected only after the intervention has taken place. Unlike controlled experiments, there is no comparison group. This design is useful when researchers cannot administer a pre-test or when it is logistically difficult to do so.
Example : Suppose you want to assess the effectiveness of a new time management seminar. You offer the seminar to a group of employees and measure their productivity levels immediately afterward to determine if there's an observable impact.
One-Group Pretest-Posttest Design
Similar to the One-Group Posttest-Only Design, this approach includes a pre-test measure in addition to the post-test. Researchers collect data both before and after the intervention. By comparing the pre-test and post-test results within the same group, you can gain a better understanding of the changes that occur due to the independent variable.
Example : If you're studying the impact of a stress management program on participants' stress levels, you would measure their stress levels before the program (pre-test) and after completing the program (post-test) to assess any changes.
Non-Equivalent Groups Design
The Non-Equivalent Groups Design involves multiple groups, but they are not randomly assigned. Instead, researchers must carefully match or control for relevant variables to minimize biases. This design is particularly useful when random assignment is not possible or ethical.
Example : Imagine you're examining the effectiveness of two teaching methods in two different schools. You can't randomly assign students to the schools, but you can carefully match them based on factors like age, prior academic performance, and socioeconomic status to create equivalent groups.
Time Series Design
Time Series Design is an approach where data is collected at multiple time points before and after the intervention. This design allows researchers to analyze trends and patterns over time, providing valuable insights into the sustained effects of the independent variable.
Example : If you're studying the impact of a new marketing campaign on product sales, you would collect sales data at regular intervals (e.g., monthly) before and after the campaign's launch to observe any long-term trends.
Regression Discontinuity Design
Regression Discontinuity Design is employed when participants are assigned to different groups based on a specific cutoff score or threshold. This design is often used in educational and policy research to assess the effects of interventions near a cutoff point.
Example : Suppose you're evaluating the impact of a scholarship program on students' academic performance. Students who score just above or below a certain GPA threshold are assigned differently to the program. This design helps assess the program's effectiveness at the cutoff point.
Propensity Score Matching
Propensity Score Matching is a technique used to create comparable treatment and control groups in non-randomized studies. Researchers calculate propensity scores based on participants' characteristics and match individuals in the treatment group to those in the control group with similar scores.
Example : If you're studying the effects of a new medication on patient outcomes, you would use propensity scores to match patients who received the medication with those who did not but have similar health profiles.
Interrupted Time Series Design
The Interrupted Time Series Design involves collecting data at multiple time points before and after the introduction of an intervention. However, in this design, the intervention occurs at a specific point in time, allowing researchers to assess its immediate impact.
Example : Let's say you're analyzing the effects of a new traffic management system on traffic accidents. You collect accident data before and after the system's implementation to observe any abrupt changes right after its introduction.
Each of these quasi-experimental designs offers unique advantages and is best suited to specific research questions and scenarios. Choosing the right design is crucial for conducting robust and informative studies.
Advantages and Disadvantages of Quasi-Experimental Design
Quasi-experimental design offers a valuable research approach, but like any methodology, it comes with its own set of advantages and disadvantages. Let's explore these in detail.
Quasi-Experimental Design Advantages
Quasi-experimental design presents several advantages that make it a valuable tool in research:
- Real-World Applicability: Quasi-experimental studies often take place in real-world settings, making the findings more applicable to practical situations. Researchers can examine the effects of interventions or variables in the context where they naturally occur.
- Ethical Considerations: In situations where manipulating the independent variable in a controlled experiment would be unethical, quasi-experimental design provides an ethical alternative. For example, it would be unethical to assign participants to smoke for a study on the health effects of smoking, but you can study naturally occurring groups of smokers and non-smokers.
- Cost-Efficiency: Conducting Quasi-Experimental research is often more cost-effective than conducting controlled experiments. The absence of controlled environments and extensive manipulations can save both time and resources.
These advantages make quasi-experimental design an attractive choice for researchers facing practical or ethical constraints in their studies.
Quasi-Experimental Design Disadvantages
However, quasi-experimental design also comes with its share of challenges and disadvantages:
- Limited Control: Unlike controlled experiments, where researchers have full control over variables, quasi-experimental design lacks the same level of control. This limited control can result in confounding variables that make it difficult to establish causality.
- Threats to Internal Validity: Various threats to internal validity, such as selection bias, history effects, and maturation effects, can compromise the accuracy of causal inferences. Researchers must carefully address these threats to ensure the validity of their findings.
- Causality Inference Challenges: Establishing causality can be challenging in quasi-experimental design due to the absence of randomization and control. While you can make strong arguments for causality, it may not be as conclusive as in controlled experiments.
- Potential Confounding Variables: In a quasi-experimental design, it's often challenging to control for all possible confounding variables that may affect the dependent variable. This can lead to uncertainty in attributing changes solely to the independent variable.
Despite these disadvantages, quasi-experimental design remains a valuable research tool when used judiciously and with a keen awareness of its limitations. Researchers should carefully consider their research questions and the practical constraints they face before choosing this approach.
How to Conduct a Quasi-Experimental Study?
Conducting a Quasi-Experimental study requires careful planning and execution to ensure the validity of your research. Let's dive into the essential steps you need to follow when conducting such a study.
1. Define Research Questions and Objectives
The first step in any research endeavor is clearly defining your research questions and objectives. This involves identifying the independent variable (IV) and the dependent variable (DV) you want to study. What is the specific relationship you want to explore, and what do you aim to achieve with your research?
- Specify Your Research Questions : Start by formulating precise research questions that your study aims to answer. These questions should be clear, focused, and relevant to your field of study.
- Identify the Independent Variable: Define the variable you intend to manipulate or study in your research. Understand its significance in your study's context.
- Determine the Dependent Variable: Identify the outcome or response variable that will be affected by changes in the independent variable.
- Establish Hypotheses (If Applicable): If you have specific hypotheses about the relationship between the IV and DV, state them clearly. Hypotheses provide a framework for testing your research questions.
2. Select the Appropriate Quasi-Experimental Design
Choosing the right quasi-experimental design is crucial for achieving your research objectives. Select a design that aligns with your research questions and the available data. Consider factors such as the feasibility of implementing the design and the ethical considerations involved.
- Evaluate Your Research Goals: Assess your research questions and objectives to determine which type of quasi-experimental design is most suitable. Each design has its strengths and limitations, so choose one that aligns with your goals.
- Consider Ethical Constraints: Take into account any ethical concerns related to your research. Depending on your study's context, some designs may be more ethically sound than others.
- Assess Data Availability: Ensure you have access to the necessary data for your chosen design. Some designs may require extensive historical data, while others may rely on data collected during the study.
3. Identify and Recruit Participants
Selecting the right participants is a critical aspect of Quasi-Experimental research. The participants should represent the population you want to make inferences about, and you must address ethical considerations, including informed consent.
- Define Your Target Population: Determine the population that your study aims to generalize to. Your sample should be representative of this population.
- Recruitment Process: Develop a plan for recruiting participants. Depending on your design, you may need to reach out to specific groups or institutions.
- Informed Consent: Ensure that you obtain informed consent from participants. Clearly explain the nature of the study, potential risks, and their rights as participants.
4. Collect Data
Data collection is a crucial step in Quasi-Experimental research. You must adhere to a consistent and systematic process to gather relevant information before and after the intervention or treatment.
- Pre-Test Measures: If applicable, collect data before introducing the independent variable. Ensure that the pre-test measures are standardized and reliable.
- Post-Test Measures: After the intervention, collect post-test data using the same measures as the pre-test. This allows you to assess changes over time.
- Maintain Data Consistency: Ensure that data collection procedures are consistent across all participants and time points to minimize biases.
5. Analyze Data
Once you've collected your data, it's time to analyze it using appropriate statistical techniques . The choice of analysis depends on your research questions and the type of data you've gathered.
- Statistical Analysis : Use statistical software to analyze your data. Common techniques include t-tests , analysis of variance (ANOVA) , regression analysis , and more, depending on the design and variables.
- Control for Confounding Variables: Be aware of potential confounding variables and include them in your analysis as covariates to ensure accurate results.
Chi-Square Calculator :
t-Test Calculator :
6. Interpret Results
With the analysis complete, you can interpret the results to draw meaningful conclusions about the relationship between the independent and dependent variables.
- Examine Effect Sizes: Assess the magnitude of the observed effects to determine their practical significance.
- Consider Significance Levels: Determine whether the observed results are statistically significant . Understand the p-values and their implications.
- Compare Findings to Hypotheses: Evaluate whether your findings support or reject your hypotheses and research questions.
7. Draw Conclusions
Based on your analysis and interpretation of the results, draw conclusions about the research questions and objectives you set out to address.
- Causal Inferences: Discuss the extent to which your study allows for causal inferences. Be transparent about the limitations and potential alternative explanations for your findings.
- Implications and Applications: Consider the practical implications of your research. How do your findings contribute to existing knowledge, and how can they be applied in real-world contexts?
- Future Research: Identify areas for future research and potential improvements in study design. Highlight any limitations or constraints that may have affected your study's outcomes.
By following these steps meticulously, you can conduct a rigorous and informative Quasi-Experimental study that advances knowledge in your field of research.
Quasi-Experimental Design Examples
Quasi-experimental design finds applications in a wide range of research domains, including business-related and market research scenarios. Below, we delve into some detailed examples of how this research methodology is employed in practice:
Example 1: Assessing the Impact of a New Marketing Strategy
Suppose a company wants to evaluate the effectiveness of a new marketing strategy aimed at boosting sales. Conducting a controlled experiment may not be feasible due to the company's existing customer base and the challenge of randomly assigning customers to different marketing approaches. In this scenario, a quasi-experimental design can be employed.
- Independent Variable: The new marketing strategy.
- Dependent Variable: Sales revenue.
- Design: The company could implement the new strategy for one group of customers while maintaining the existing strategy for another group. Both groups are selected based on similar demographics and purchase history , reducing selection bias. Pre-implementation data (sales records) can serve as the baseline, and post-implementation data can be collected to assess the strategy's impact.
Example 2: Evaluating the Effectiveness of Employee Training Programs
In the context of human resources and employee development, organizations often seek to evaluate the impact of training programs. A randomized controlled trial (RCT) with random assignment may not be practical or ethical, as some employees may need specific training more than others. Instead, a quasi-experimental design can be employed.
- Independent Variable: Employee training programs.
- Dependent Variable: Employee performance metrics, such as productivity or quality of work.
- Design: The organization can offer training programs to employees who express interest or demonstrate specific needs, creating a self-selected treatment group. A comparable control group can consist of employees with similar job roles and qualifications who did not receive the training. Pre-training performance metrics can serve as the baseline, and post-training data can be collected to assess the impact of the training programs.
Example 3: Analyzing the Effects of a Tax Policy Change
In economics and public policy, researchers often examine the effects of tax policy changes on economic behavior. Conducting a controlled experiment in such cases is practically impossible. Therefore, a quasi-experimental design is commonly employed.
- Independent Variable: Tax policy changes (e.g., tax rate adjustments).
- Dependent Variable: Economic indicators, such as consumer spending or business investments.
- Design: Researchers can analyze data from different regions or jurisdictions where tax policy changes have been implemented. One region could represent the treatment group (with tax policy changes), while a similar region with no tax policy changes serves as the control group. By comparing economic data before and after the policy change in both groups, researchers can assess the impact of the tax policy changes.
These examples illustrate how quasi-experimental design can be applied in various research contexts, providing valuable insights into the effects of independent variables in real-world scenarios where controlled experiments are not feasible or ethical. By carefully selecting comparison groups and controlling for potential biases, researchers can draw meaningful conclusions and inform decision-making processes.
How to Publish Quasi-Experimental Research?
Publishing your Quasi-Experimental research findings is a crucial step in contributing to the academic community's knowledge. We'll explore the essential aspects of reporting and publishing your Quasi-Experimental research effectively.
Structuring Your Research Paper
When preparing your research paper, it's essential to adhere to a well-structured format to ensure clarity and comprehensibility. Here are key elements to include:
Title and Abstract
- Title: Craft a concise and informative title that reflects the essence of your study. It should capture the main research question or hypothesis.
- Abstract: Summarize your research in a structured abstract, including the purpose, methods, results, and conclusions. Ensure it provides a clear overview of your study.
Introduction
- Background and Rationale: Provide context for your study by discussing the research gap or problem your study addresses. Explain why your research is relevant and essential.
- Research Questions or Hypotheses: Clearly state your research questions or hypotheses and their significance.
Literature Review
- Review of Related Work: Discuss relevant literature that supports your research. Highlight studies with similar methodologies or findings and explain how your research fits within this context.
- Participants: Describe your study's participants, including their characteristics and how you recruited them.
- Quasi-Experimental Design: Explain your chosen design in detail, including the independent and dependent variables, procedures, and any control measures taken.
- Data Collection: Detail the data collection methods , instruments used, and any pre-test or post-test measures.
- Data Analysis: Describe the statistical techniques employed, including any control for confounding variables.
- Presentation of Findings: Present your results clearly, using tables, graphs, and descriptive statistics where appropriate. Include p-values and effect sizes, if applicable.
- Interpretation of Results: Discuss the implications of your findings and how they relate to your research questions or hypotheses.
- Interpretation and Implications: Analyze your results in the context of existing literature and theories. Discuss the practical implications of your findings.
- Limitations: Address the limitations of your study, including potential biases or threats to internal validity.
- Future Research: Suggest areas for future research and how your study contributes to the field.
Ethical Considerations in Reporting
Ethical reporting is paramount in Quasi-Experimental research. Ensure that you adhere to ethical standards, including:
- Informed Consent: Clearly state that informed consent was obtained from all participants, and describe the informed consent process.
- Protection of Participants: Explain how you protected the rights and well-being of your participants throughout the study.
- Confidentiality: Detail how you maintained privacy and anonymity, especially when presenting individual data.
- Disclosure of Conflicts of Interest: Declare any potential conflicts of interest that could influence the interpretation of your findings.
Common Pitfalls to Avoid
When reporting your Quasi-Experimental research, watch out for common pitfalls that can diminish the quality and impact of your work:
- Overgeneralization: Be cautious not to overgeneralize your findings. Clearly state the limits of your study and the populations to which your results can be applied.
- Misinterpretation of Causality: Clearly articulate the limitations in inferring causality in Quasi-Experimental research. Avoid making strong causal claims unless supported by solid evidence.
- Ignoring Ethical Concerns: Ethical considerations are paramount. Failing to report on informed consent, ethical oversight, and participant protection can undermine the credibility of your study.
Guidelines for Transparent Reporting
To enhance the transparency and reproducibility of your Quasi-Experimental research, consider adhering to established reporting guidelines, such as:
- CONSORT Statement: If your study involves interventions or treatments, follow the CONSORT guidelines for transparent reporting of randomized controlled trials.
- STROBE Statement: For observational studies, the STROBE statement provides guidance on reporting essential elements.
- PRISMA Statement: If your research involves systematic reviews or meta-analyses, adhere to the PRISMA guidelines.
- Transparent Reporting of Evaluations with Non-Randomized Designs (TREND): TREND guidelines offer specific recommendations for transparently reporting non-randomized designs, including Quasi-Experimental research.
By following these reporting guidelines and maintaining the highest ethical standards, you can contribute to the advancement of knowledge in your field and ensure the credibility and impact of your Quasi-Experimental research findings.
Quasi-Experimental Design Challenges
Conducting a Quasi-Experimental study can be fraught with challenges that may impact the validity and reliability of your findings. We'll take a look at some common challenges and provide strategies on how you can address them effectively.
Selection Bias
Challenge: Selection bias occurs when non-randomized groups differ systematically in ways that affect the study's outcome. This bias can undermine the validity of your research, as it implies that the groups are not equivalent at the outset of the study.
Addressing Selection Bias:
- Matching: Employ matching techniques to create comparable treatment and control groups. Match participants based on relevant characteristics, such as age, gender, or prior performance, to balance the groups.
- Statistical Controls: Use statistical controls to account for differences between groups. Include covariates in your analysis to adjust for potential biases.
- Sensitivity Analysis: Conduct sensitivity analyses to assess how vulnerable your results are to selection bias. Explore different scenarios to understand the impact of potential bias on your conclusions.

History Effects
Challenge: History effects refer to external events or changes over time that influence the study's results. These external factors can confound your research by introducing variables you did not account for.
Addressing History Effects:
- Collect Historical Data: Gather extensive historical data to understand trends and patterns that might affect your study. By having a comprehensive historical context, you can better identify and account for historical effects.
- Control Groups: Include control groups whenever possible. By comparing the treatment group's results to those of a control group, you can account for external influences that affect both groups equally.
- Time Series Analysis : If applicable, use time series analysis to detect and account for temporal trends. This method helps differentiate between the effects of the independent variable and external events.
Maturation Effects
Challenge: Maturation effects occur when participants naturally change or develop throughout the study, independent of the intervention. These changes can confound your results, making it challenging to attribute observed effects solely to the independent variable.
Addressing Maturation Effects:
- Randomization: If possible, use randomization to distribute maturation effects evenly across treatment and control groups. Random assignment minimizes the impact of maturation as a confounding variable.
- Matched Pairs: If randomization is not feasible, employ matched pairs or statistical controls to ensure that both groups experience similar maturation effects.
- Shorter Time Frames: Limit the duration of your study to reduce the likelihood of significant maturation effects. Shorter studies are less susceptible to long-term maturation.
Regression to the Mean
Challenge: Regression to the mean is the tendency for extreme scores on a variable to move closer to the mean upon retesting. This can create the illusion of an intervention's effectiveness when, in reality, it's a natural statistical phenomenon.
Addressing Regression to the Mean:
- Use Control Groups: Include control groups in your study to provide a baseline for comparison. This helps differentiate genuine intervention effects from regression to the mean.
- Multiple Data Points: Collect numerous data points to identify patterns and trends. If extreme scores regress to the mean in subsequent measurements, it may be indicative of regression to the mean rather than a true intervention effect.
- Statistical Analysis: Employ statistical techniques that account for regression to the mean when analyzing your data. Techniques like analysis of covariance (ANCOVA) can help control for baseline differences.
Attrition and Mortality
Challenge: Attrition refers to the loss of participants over the course of your study, while mortality is the permanent loss of participants. High attrition rates can introduce biases and affect the representativeness of your sample.
Addressing Attrition and Mortality:
- Careful Participant Selection: Select participants who are likely to remain engaged throughout the study. Consider factors that may lead to attrition, such as participant motivation and commitment.
- Incentives: Provide incentives or compensation to participants to encourage their continued participation.
- Follow-Up Strategies: Implement effective follow-up strategies to reduce attrition. Regular communication and reminders can help keep participants engaged.
- Sensitivity Analysis: Conduct sensitivity analyses to assess the impact of attrition and mortality on your results. Compare the characteristics of participants who dropped out with those who completed the study.
Testing Effects
Challenge: Testing effects occur when the mere act of testing or assessing participants affects their subsequent performance. This phenomenon can lead to changes in the dependent variable that are unrelated to the independent variable.
Addressing Testing Effects:
- Counterbalance Testing: If possible, counterbalance the order of tests or assessments between treatment and control groups. This helps distribute the testing effects evenly across groups.
- Control Groups: Include control groups subjected to the same testing or assessment procedures as the treatment group. By comparing the two groups, you can determine whether testing effects have influenced the results.
- Minimize Testing Frequency: Limit the frequency of testing or assessments to reduce the likelihood of testing effects. Conducting fewer assessments can mitigate the impact of repeated testing on participants.
By proactively addressing these common challenges, you can enhance the validity and reliability of your Quasi-Experimental study, making your findings more robust and trustworthy.
Conclusion for Quasi-Expermental Design
Quasi-experimental design is a powerful tool that helps researchers investigate cause-and-effect relationships in real-world situations where strict control is not always possible. By understanding the key concepts, types of designs, and how to address challenges, you can conduct robust research and contribute valuable insights to your field. Remember, quasi-experimental design bridges the gap between controlled experiments and purely observational studies, making it an essential approach in various fields, from business and market research to public policy and beyond. So, whether you're a researcher, student, or decision-maker, the knowledge of quasi-experimental design empowers you to make informed choices and drive positive changes in the world.
How to Supercharge Quasi-Experimental Design with Real-Time Insights?
Introducing Appinio , the real-time market research platform that transforms the world of quasi-experimental design. Imagine having the power to conduct your own market research in minutes, obtaining actionable insights that fuel your data-driven decisions. Appinio takes care of the research and tech complexities, freeing you to focus on what truly matters for your business.
Here's why Appinio stands out:
- Lightning-Fast Insights: From formulating questions to uncovering insights, Appinio delivers results in minutes, ensuring you get the answers you need when you need them.
- No Research Degree Required: Our intuitive platform is designed for everyone, eliminating the need for a PhD in research. Anyone can dive in and start harnessing the power of real-time consumer insights.
- Global Reach, Local Expertise: With access to over 90 countries and the ability to define precise target groups based on 1200+ characteristics, you can conduct Quasi-Experimental research on a global scale while maintaining a local touch.
Get free access to the platform!
Join the loop 💌
Be the first to hear about new updates, product news, and data insights. We'll send it all straight to your inbox.
Get the latest market research news straight to your inbox! 💌
Wait, there's more

19.09.2024 | 9min read
Track Your Customer Retention & Brand Metrics for Post-Holiday Success

16.09.2024 | 10min read
Creative Checkup – Optimize Advertising Slogans & Creatives for ROI

03.09.2024 | 10min read
Get your brand Holiday Ready: 4 Essential Steps to Smash your Q4
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Methodology
- Independent vs. Dependent Variables | Definition & Examples
Independent vs. Dependent Variables | Definition & Examples
Published on February 3, 2022 by Pritha Bhandari . Revised on June 22, 2023.
In research, variables are any characteristics that can take on different values, such as height, age, temperature, or test scores.
Researchers often manipulate or measure independent and dependent variables in studies to test cause-and-effect relationships.
- The independent variable is the cause. Its value is independent of other variables in your study.
- The dependent variable is the effect. Its value depends on changes in the independent variable.
Your independent variable is the temperature of the room. You vary the room temperature by making it cooler for half the participants, and warmer for the other half.
Table of contents
What is an independent variable, types of independent variables, what is a dependent variable, identifying independent vs. dependent variables, independent and dependent variables in research, visualizing independent and dependent variables, other interesting articles, frequently asked questions about independent and dependent variables.
An independent variable is the variable you manipulate or vary in an experimental study to explore its effects. It’s called “independent” because it’s not influenced by any other variables in the study.
Independent variables are also called:
- Explanatory variables (they explain an event or outcome)
- Predictor variables (they can be used to predict the value of a dependent variable)
- Right-hand-side variables (they appear on the right-hand side of a regression equation).
These terms are especially used in statistics , where you estimate the extent to which an independent variable change can explain or predict changes in the dependent variable.
Prevent plagiarism. Run a free check.
There are two main types of independent variables.
- Experimental independent variables can be directly manipulated by researchers.
- Subject variables cannot be manipulated by researchers, but they can be used to group research subjects categorically.
Experimental variables
In experiments, you manipulate independent variables directly to see how they affect your dependent variable. The independent variable is usually applied at different levels to see how the outcomes differ.
You can apply just two levels in order to find out if an independent variable has an effect at all.
You can also apply multiple levels to find out how the independent variable affects the dependent variable.
You have three independent variable levels, and each group gets a different level of treatment.
You randomly assign your patients to one of the three groups:
- A low-dose experimental group
- A high-dose experimental group
- A placebo group (to research a possible placebo effect )
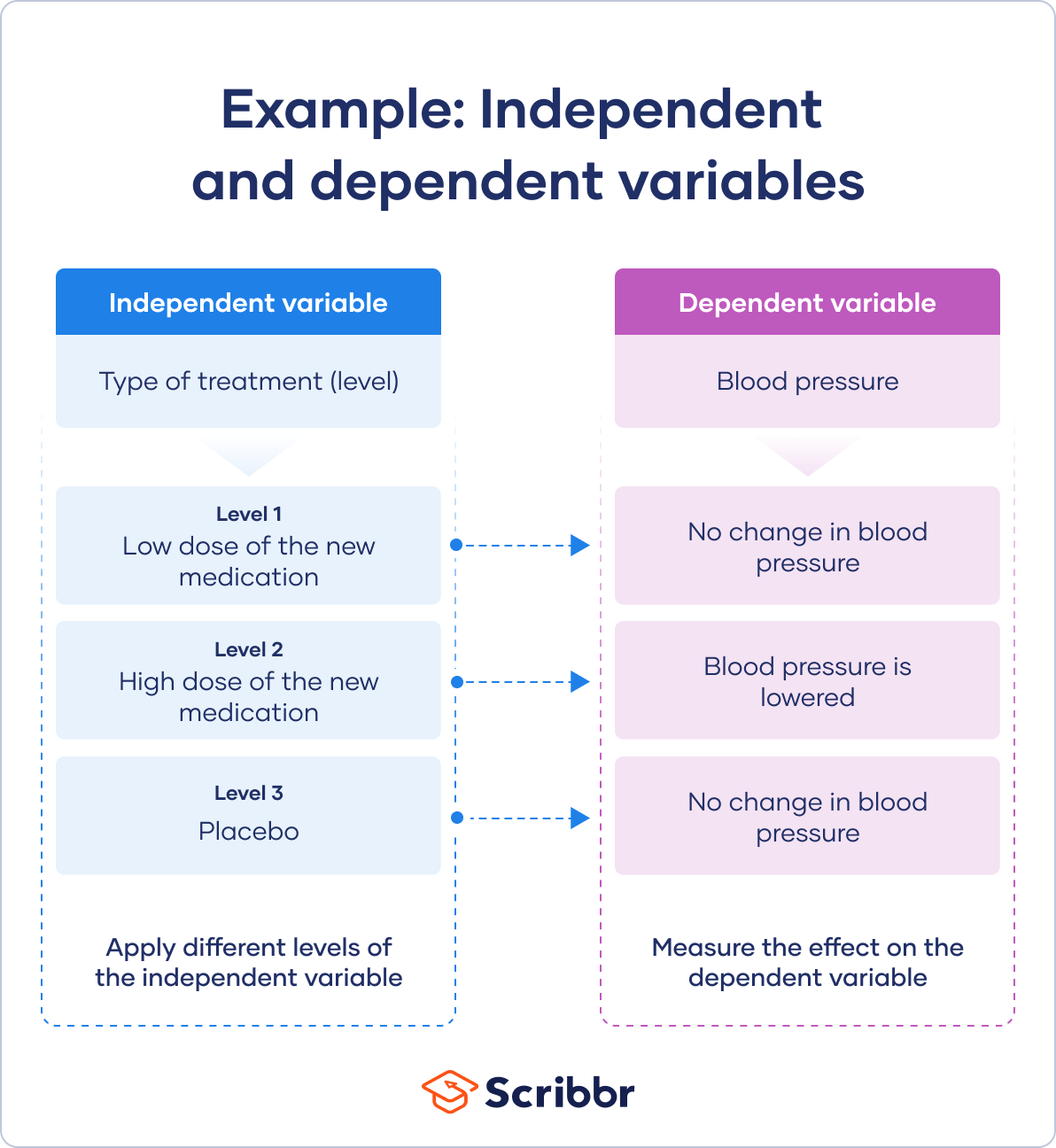
A true experiment requires you to randomly assign different levels of an independent variable to your participants.
Random assignment helps you control participant characteristics, so that they don’t affect your experimental results. This helps you to have confidence that your dependent variable results come solely from the independent variable manipulation.
Subject variables
Subject variables are characteristics that vary across participants, and they can’t be manipulated by researchers. For example, gender identity, ethnicity, race, income, and education are all important subject variables that social researchers treat as independent variables.
It’s not possible to randomly assign these to participants, since these are characteristics of already existing groups. Instead, you can create a research design where you compare the outcomes of groups of participants with characteristics. This is a quasi-experimental design because there’s no random assignment. Note that any research methods that use non-random assignment are at risk for research biases like selection bias and sampling bias .
Your independent variable is a subject variable, namely the gender identity of the participants. You have three groups: men, women and other.
Your dependent variable is the brain activity response to hearing infant cries. You record brain activity with fMRI scans when participants hear infant cries without their awareness.
A dependent variable is the variable that changes as a result of the independent variable manipulation. It’s the outcome you’re interested in measuring, and it “depends” on your independent variable.
In statistics , dependent variables are also called:
- Response variables (they respond to a change in another variable)
- Outcome variables (they represent the outcome you want to measure)
- Left-hand-side variables (they appear on the left-hand side of a regression equation)
The dependent variable is what you record after you’ve manipulated the independent variable. You use this measurement data to check whether and to what extent your independent variable influences the dependent variable by conducting statistical analyses.
Based on your findings, you can estimate the degree to which your independent variable variation drives changes in your dependent variable. You can also predict how much your dependent variable will change as a result of variation in the independent variable.
Distinguishing between independent and dependent variables can be tricky when designing a complex study or reading an academic research paper .
A dependent variable from one study can be the independent variable in another study, so it’s important to pay attention to research design .
Here are some tips for identifying each variable type.
Recognizing independent variables
Use this list of questions to check whether you’re dealing with an independent variable:
- Is the variable manipulated, controlled, or used as a subject grouping method by the researcher?
- Does this variable come before the other variable in time?
- Is the researcher trying to understand whether or how this variable affects another variable?
Recognizing dependent variables
Check whether you’re dealing with a dependent variable:
- Is this variable measured as an outcome of the study?
- Is this variable dependent on another variable in the study?
- Does this variable get measured only after other variables are altered?
Independent and dependent variables are generally used in experimental and quasi-experimental research.
Here are some examples of research questions and corresponding independent and dependent variables.
| Research question | Independent variable | Dependent variable(s) |
|---|---|---|
| Do tomatoes grow fastest under fluorescent, incandescent, or natural light? | ||
| What is the effect of intermittent fasting on blood sugar levels? | ||
| Is medical marijuana effective for pain reduction in people with chronic pain? | ||
| To what extent does remote working increase job satisfaction? |
For experimental data, you analyze your results by generating descriptive statistics and visualizing your findings. Then, you select an appropriate statistical test to test your hypothesis .
The type of test is determined by:
- your variable types
- level of measurement
- number of independent variable levels.
You’ll often use t tests or ANOVAs to analyze your data and answer your research questions.
In quantitative research , it’s good practice to use charts or graphs to visualize the results of studies. Generally, the independent variable goes on the x -axis (horizontal) and the dependent variable on the y -axis (vertical).
The type of visualization you use depends on the variable types in your research questions:
- A bar chart is ideal when you have a categorical independent variable.
- A scatter plot or line graph is best when your independent and dependent variables are both quantitative.
To inspect your data, you place your independent variable of treatment level on the x -axis and the dependent variable of blood pressure on the y -axis.
You plot bars for each treatment group before and after the treatment to show the difference in blood pressure.
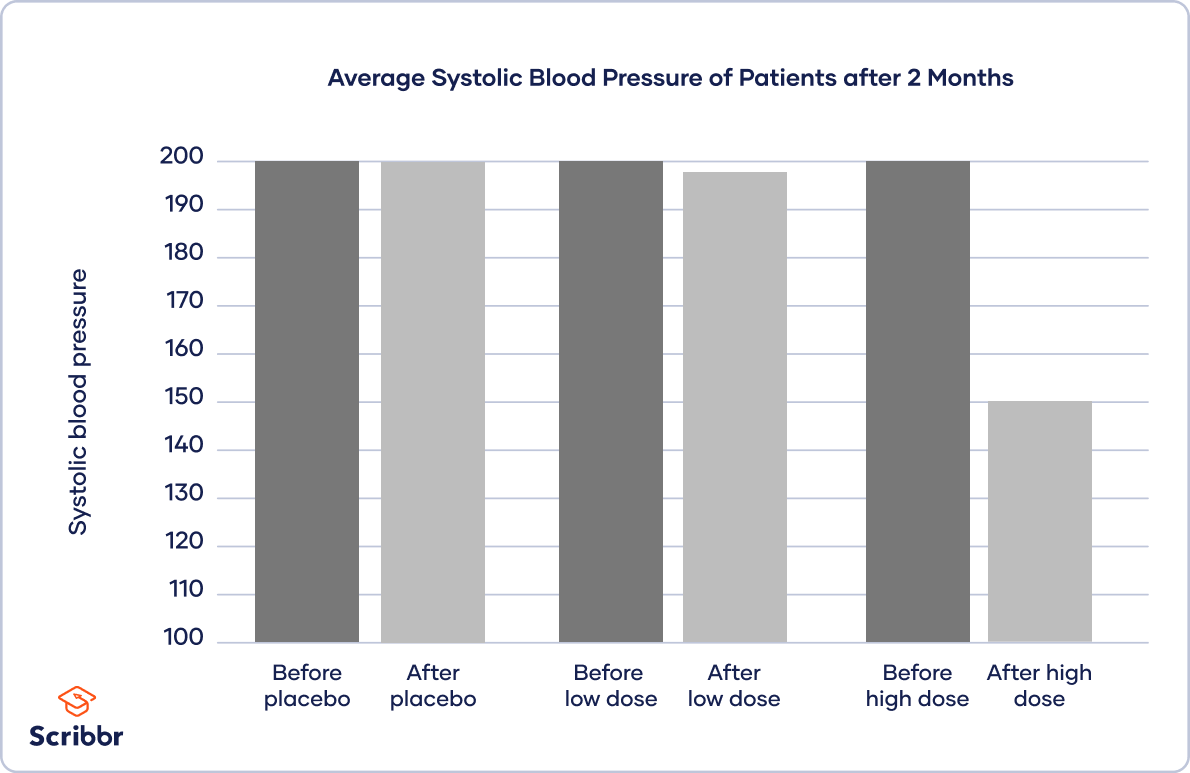
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Degrees of freedom
- Null hypothesis
- Discourse analysis
- Control groups
- Mixed methods research
- Non-probability sampling
- Quantitative research
- Ecological validity
Research bias
- Rosenthal effect
- Implicit bias
- Cognitive bias
- Selection bias
- Negativity bias
- Status quo bias
An independent variable is the variable you manipulate, control, or vary in an experimental study to explore its effects. It’s called “independent” because it’s not influenced by any other variables in the study.
A dependent variable is what changes as a result of the independent variable manipulation in experiments . It’s what you’re interested in measuring, and it “depends” on your independent variable.
In statistics, dependent variables are also called:
Determining cause and effect is one of the most important parts of scientific research. It’s essential to know which is the cause – the independent variable – and which is the effect – the dependent variable.
You want to find out how blood sugar levels are affected by drinking diet soda and regular soda, so you conduct an experiment .
- The type of soda – diet or regular – is the independent variable .
- The level of blood sugar that you measure is the dependent variable – it changes depending on the type of soda.
No. The value of a dependent variable depends on an independent variable, so a variable cannot be both independent and dependent at the same time. It must be either the cause or the effect, not both!
Yes, but including more than one of either type requires multiple research questions .
For example, if you are interested in the effect of a diet on health, you can use multiple measures of health: blood sugar, blood pressure, weight, pulse, and many more. Each of these is its own dependent variable with its own research question.
You could also choose to look at the effect of exercise levels as well as diet, or even the additional effect of the two combined. Each of these is a separate independent variable .
To ensure the internal validity of an experiment , you should only change one independent variable at a time.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bhandari, P. (2023, June 22). Independent vs. Dependent Variables | Definition & Examples. Scribbr. Retrieved October 17, 2024, from https://www.scribbr.com/methodology/independent-and-dependent-variables/
Is this article helpful?

Pritha Bhandari
Other students also liked, guide to experimental design | overview, steps, & examples, explanatory and response variables | definitions & examples, confounding variables | definition, examples & controls, "i thought ai proofreading was useless but..".
I've been using Scribbr for years now and I know it's a service that won't disappoint. It does a good job spotting mistakes”
Research Methods Course Pack
Chapter 10 moderating, mediating, and confounding variables, 10.1 more than the iv and the dv.
In this section, we’ll expand our understanding of variables in the study. So far, we have discussed three types of variables:
Independent variable (IV): The variable that is implied (quasi-experiment, non-experiment) or demonstrated to be (experiment) the cause of an effect. When there is a manipulation, the variable that is manipulated is the IV.
Dependent variable (DV): The variable that is implied or demonstrated to be the outcome.
Confounding variable: Also called a nuisance variable or third variable. This is a third variable that causes a change in both the IV and the DV at the same time. To borrow an example, we might observe a correlation between ice cream consumption and snake bites. We might wonder if eating ice cream causes snake bites on the basis of this result. Although this seems ridiculous, it’s easier for us to make these sorts of conclusions when the variables are psychological constructs (for example, personality and job outcomes). In this example, the weather is a confounding variable. When the weather is warmer, ice cream consumption (it’s warm) and snake bites (people go on hikes) increase.
From this example, you might wonder if other factors matter, such as the location (regions with lots of snakes versus regions with fewer). Some of these other variables may affect the DV in other ways, such as by weakening the relationship between the IV and the DV. Therefore, confounding variables are one type of extraneous variable. Extraneous variables include anything we have not included in our study.
Some extraneous variables are not likely to affect anything. In this example, the gender of people buying ice cream probably does not affect their likelihood of snake bites. Other extraneous variables can affect the relationship we are trying to observe in our study. Whenever you design a study, an important step is to stop and consider “what else could be affecting this relationship?” When you do this, you will brainstorm a list of possible confounding and extraneous variables. Then, you’ll decide if the variables are likely to affect the relationship of interest. If they are, then usually you can redesign your study to avoid them.
To summarize: A study is essentially a search to identify and explain relationships between IVs and DVs. When claims about the relationship between an IV and DV are true, the claim has internal validity.
Next, we will explore two more complex relationships between variables that develop when we add a second IV to our model.
10.2 Moderating Variables: Interaction Effects
Interactions are also called moderated relationships or moderation. An interaction occurs when the effect of one variable depends on the value of another variable. ** For example, how do you increase the sweetness of coffee? Imagine that sweetness is the DV, and the two variables are stirring (yes vs no) and adding a sugar cube (yes vs no).
We diagram a moderated relationship using this notation:

Diagram of a moderated relationship with IV 2 and IV 1 interacting to affect DV
And, when we have group means for every condition, we can see the impact of these two factors (factor is a fancy word for IV) in a table:
| . | Stirring: Yes | Stirring: No |
|---|---|---|
| Sugar: Yes | \(\bar{X}_{sweet}=100\) | \(\bar{X}_{sweet} = 0\) |
| Sugar: No | \(\bar{X}_{sweet}=0\) | \(\bar{X}_{sweet} = 0\) |
When is the coffee sweet? Stirring alone does not change the taste of the coffee. Adding a sugar cube alone also doesn’t change the taste of the coffee, since the sugar will just sink to the bottom. It’s only when sugar is added, and the coffee is stirred that it tastes sweet.
We can say there is an interaction between adding sugar and stirring coffee. The effect of the stirring depends on the value of another variable (whether or not sugar is added).
10.3 Some Terminology
When more than one IV is included in a model, we are using a factorial design. Factorial designs include 2 or more factors (or IVs) with 2 or more levels each. In the coffee example, our design has two factors (stirring and adding sugar), each with two levels.
In factorial designs (i.e., studies that manipulate two or more factors), participants are observed at each level of each factor. Because every possible combination of each IV is included, the effects of each factor alone can be observed. We also get to see how these factors impact each other. We say this design is fully crossed because every possible combination of levels is included.
10.4 Main Effects
A main effect is the effect of one factor. There is one potential main effect for each factor.
In this example, the potential main effects are stirring and adding sugar. To find the main effects, find the mean of each column (i.e., add the two numbers and divide by 2). If there are differences in these means, there is a significant main effect for one of the factors. Next, find the mean of each row (add going across and divide by 2). If there are differences in these row means, then there is a main effect for the other factor.
| . | Stirring: Yes | Stirring: No | Row mean |
|---|---|---|---|
| Sugar: Yes | \(\bar{X}_{sweet}=100\) | \(\bar{X}_{sweet} = 0\) | \(\bar{X}_{sugar}= 50\) |
| Sugar: No | \(\bar{X}_{sweet}=0\) | \(\bar{X}_{sweet} = 0\) | \(\bar{X}_{\text{no sugar}}=0\) |
| Column mean | \(\bar{X}_{stir}=50\) | \(\bar{X}_{nostir}=0\) . |
In our example, we see two main effects. Adding a sugar cube (mean of 50) differs from not adding sugar (mean of 0). That’s the first main effect. The second is stirring; stirring (mean of 50) differs from not stirring (mean of 0).
10.5 Simple Effects
When an interaction effect is present, each part of an interaction is called a simple effect. To examine the simple effects, compare each cell to every other cell in the same row. Next, compare each cell to ever other cell in the same column. Simple effects are never diagonal from each other.
In our example, we see a simple effect as we go from Stir+Sugar to NoStir+Sugar. There is no simple effect between Stir+NoSugar and NoStir+NoSugar (both are 0). What makes this an interaction effect is that these two simple effects are different from one another.
On the vertical, there is a simple effect from Stir+Sugar to Stir+NoSugar. There is no simple effect from NoStir+Sugar to NoStir+NoSugar (both are 0). Again, this is an interaction effect because these two simple effects are different.
10.6 Interaction Effect
When there is at least one (significant) simple effect that differs across levels of one of the IVs (as demonstrated above), then you can say there is an interaction between the two factors. In a two-way ANOVA, there is one possible interaction effect. We sometimes show this with a multiplication symbol: Sugar*Stir. In our example, there is an interaction between sugar and stirring.
In summary: An interaction effect is when the impact of one variable depends on the level of another variable.
Interaction effects are important in psychology because they let us explain the circumstances under which an effect occurs. Anytime we say that an effect depends on something else, we are describing an interaction effect.
10.7 Mediators and Mediated Relationships
A mediated relationship is a chain reaction; one variable causes another variable (the mediator), which then causes the DV. Please forgive another silly example; I am including it to keep the example as simple as possible. Here is how we diagram it:

This is a totally different situation that the previous one. The first variable is a preference for sweetness; do you like sweet foods and beverages? If participants prefer sweetness, then they will add more sugar. If they don’t prefer sugar in their coffee, then they will add less (or no) sugar. Thus, preference for sweetness is an IV that causes a change in the mediator, adding sugar. Finally, adding sugar is what causes the coffee to taste sweet. Any time we can string together three variables in a causal chain, we are describing a mediated relationship.
In summary: A mediated relationship occurs when one variable affects another (the mediator), and that variable (the mediator), affects something else.
Mediated relationships are important in psychology because they let us explain why or how an effect happens. The mediator is the how or the why. Why do participants who prefer sweetness end up with sweeter coffee? It is because they added sugar.
Reference Library
Collections
- See what's new
- All Resources
- Student Resources
- Assessment Resources
- Teaching Resources
- CPD Courses
- Livestreams
Study notes, videos, interactive activities and more!
Psychology news, insights and enrichment
Currated collections of free resources
Browse resources by topic
- All Psychology Resources
Resource Selections
Currated lists of resources
Quasi Experiment
Quasi-experiments contain a naturally occurring IV. However, in a quasi-experiment the naturally occurring IV is a difference between people that already exists (i.e. gender, age). The researcher examines the effect of this variable on the dependent variable (DV).
- Share on Facebook
- Share on Twitter
- Share by Email
Types of Experiment: Overview
Study Notes
Research Methods: MCQ Revision Test 1 for AQA A Level Psychology
Topic Videos
Example Answers for Research Methods: A Level Psychology, Paper 2, June 2018 (AQA)
Exam Support
A Level Psychology Topic Quiz - Research Methods
Quizzes & Activities
Our subjects
- › Criminology
- › Economics
- › Geography
- › Health & Social Care
- › Psychology
- › Sociology
- › Teaching & learning resources
- › Student revision workshops
- › Online student courses
- › CPD for teachers
- › Livestreams
- › Teaching jobs
Boston House, 214 High Street, Boston Spa, West Yorkshire, LS23 6AD Tel: 01937 848885
- › Contact us
- › Terms of use
- › Privacy & cookies
© 2002-2024 Tutor2u Limited. Company Reg no: 04489574. VAT reg no 816865400.
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Quasi Experimental Design Overview & Examples
By Jim Frost Leave a Comment
What is a Quasi Experimental Design?
A quasi experimental design is a method for identifying causal relationships that does not randomly assign participants to the experimental groups. Instead, researchers use a non-random process. For example, they might use an eligibility cutoff score or preexisting groups to determine who receives the treatment.

Quasi-experimental research is a design that closely resembles experimental research but is different. The term “quasi” means “resembling,” so you can think of it as a cousin to actual experiments. In these studies, researchers can manipulate an independent variable — that is, they change one factor to see what effect it has. However, unlike true experimental research, participants are not randomly assigned to different groups.
Learn more about Experimental Designs: Definition & Types .
When to Use Quasi-Experimental Design
Researchers typically use a quasi-experimental design because they can’t randomize due to practical or ethical concerns. For example:
- Practical Constraints : A school interested in testing a new teaching method can only implement it in preexisting classes and cannot randomly assign students.
- Ethical Concerns : A medical study might not be able to randomly assign participants to a treatment group for an experimental medication when they are already taking a proven drug.
Quasi-experimental designs also come in handy when researchers want to study the effects of naturally occurring events, like policy changes or environmental shifts, where they can’t control who is exposed to the treatment.
Quasi-experimental designs occupy a unique position in the spectrum of research methodologies, sitting between observational studies and true experiments. This middle ground offers a blend of both worlds, addressing some limitations of purely observational studies while navigating the constraints often accompanying true experiments.
A significant advantage of quasi-experimental research over purely observational studies and correlational research is that it addresses the issue of directionality, determining which variable is the cause and which is the effect. In quasi-experiments, an intervention typically occurs during the investigation, and the researchers record outcomes before and after it, increasing the confidence that it causes the observed changes.
However, it’s crucial to recognize its limitations as well. Controlling confounding variables is a larger concern for a quasi-experimental design than a true experiment because it lacks random assignment.
In sum, quasi-experimental designs offer a valuable research approach when random assignment is not feasible, providing a more structured and controlled framework than observational studies while acknowledging and attempting to address potential confounders.
Types of Quasi-Experimental Designs and Examples
Quasi-experimental studies use various methods, depending on the scenario.
Natural Experiments
This design uses naturally occurring events or changes to create the treatment and control groups. Researchers compare outcomes between those whom the event affected and those it did not affect. Analysts use statistical controls to account for confounders that the researchers must also measure.
Natural experiments are related to observational studies, but they allow for a clearer causality inference because the external event or policy change provides both a form of quasi-random group assignment and a definite start date for the intervention.
For example, in a natural experiment utilizing a quasi-experimental design, researchers study the impact of a significant economic policy change on small business growth. The policy is implemented in one state but not in neighboring states. This scenario creates an unplanned experimental setup, where the state with the new policy serves as the treatment group, and the neighboring states act as the control group.
Researchers are primarily interested in small business growth rates but need to record various confounders that can impact growth rates. Hence, they record state economic indicators, investment levels, and employment figures. By recording these metrics across the states, they can include them in the model as covariates and control them statistically. This method allows researchers to estimate differences in small business growth due to the policy itself, separate from the various confounders.
Nonequivalent Groups Design
This method involves matching existing groups that are similar but not identical. Researchers attempt to find groups that are as equivalent as possible, particularly for factors likely to affect the outcome.
For instance, researchers use a nonequivalent groups quasi-experimental design to evaluate the effectiveness of a new teaching method in improving students’ mathematics performance. A school district considering the teaching method is planning the study. Students are already divided into schools, preventing random assignment.
The researchers matched two schools with similar demographics, baseline academic performance, and resources. The school using the traditional methodology is the control, while the other uses the new approach. Researchers are evaluating differences in educational outcomes between the two methods.
They perform a pretest to identify differences between the schools that might affect the outcome and include them as covariates to control for confounding. They also record outcomes before and after the intervention to have a larger context for the changes they observe.
Regression Discontinuity
This process assigns subjects to a treatment or control group based on a predetermined cutoff point (e.g., a test score). The analysis primarily focuses on participants near the cutoff point, as they are likely similar except for the treatment received. By comparing participants just above and below the cutoff, the design controls for confounders that vary smoothly around the cutoff.
For example, in a regression discontinuity quasi-experimental design focusing on a new medical treatment for depression, researchers use depression scores as the cutoff point. Individuals with depression scores just above a certain threshold are assigned to receive the latest treatment, while those just below the threshold do not receive it. This method creates two closely matched groups: one that barely qualifies for treatment and one that barely misses out.
By comparing the mental health outcomes of these two groups over time, researchers can assess the effectiveness of the new treatment. The assumption is that the only significant difference between the groups is whether they received the treatment, thereby isolating its impact on depression outcomes.
Controlling Confounders in a Quasi-Experimental Design
Accounting for confounding variables is a challenging but essential task for a quasi-experimental design.
In a true experiment, the random assignment process equalizes confounders across the groups to nullify their overall effect. It’s the gold standard because it works on all confounders, known and unknown.
Unfortunately, the lack of random assignment can allow differences between the groups to exist before the intervention. These confounding factors might ultimately explain the results rather than the intervention.
Consequently, researchers must use other methods to equalize the groups roughly using matching and cutoff values or statistically adjust for preexisting differences they measure to reduce the impact of confounders.
A key strength of quasi-experiments is their frequent use of “pre-post testing.” This approach involves conducting initial tests before collecting data to check for preexisting differences between groups that could impact the study’s outcome. By identifying these variables early on and including them as covariates, researchers can more effectively control potential confounders in their statistical analysis.
Additionally, researchers frequently track outcomes before and after the intervention to better understand the context for changes they observe.
Statisticians consider these methods to be less effective than randomization. Hence, quasi-experiments fall somewhere in the middle when it comes to internal validity , or how well the study can identify causal relationships versus mere correlation . They’re more conclusive than correlational studies but not as solid as true experiments.
In conclusion, quasi-experimental designs offer researchers a versatile and practical approach when random assignment is not feasible. This methodology bridges the gap between controlled experiments and observational studies, providing a valuable tool for investigating cause-and-effect relationships in real-world settings. Researchers can address ethical and logistical constraints by understanding and leveraging the different types of quasi-experimental designs while still obtaining insightful and meaningful results.
Cook, T. D., & Campbell, D. T. (1979). Quasi-experimentation: Design & analysis issues in field settings . Boston, MA: Houghton Mifflin
Share this:

Reader Interactions
Comments and questions cancel reply.
- Abnormal Psychology
- Assessment (IB)
- Biological Psychology
- Cognitive Psychology
- Criminology
- Developmental Psychology
- Extended Essay
- General Interest
- Health Psychology
- Human Relationships
- IB Psychology
- IB Psychology HL Extensions
- Internal Assessment (IB)
- Love and Marriage
- Post-Traumatic Stress Disorder
- Prejudice and Discrimination
- Qualitative Research Methods
- Research Methodology
- Revision and Exam Preparation
- Social and Cultural Psychology
- Studies and Theories
- Teaching Ideas
What makes an experiment “quasi?”
Travis Dixon August 21, 2017 Research Methodology , Teaching Ideas

- Click to share on Facebook (Opens in new window)
- Click to share on Twitter (Opens in new window)
- Click to share on LinkedIn (Opens in new window)
- Click to share on Pinterest (Opens in new window)
- Click to email a link to a friend (Opens in new window)
One key characteristic of a quasi-experiment is that one or more conditions of a true experiment cannot be met. This often includes the fact that there is no random allocation to the treatment or control conditions in the experiment. So if there is no random allocation, but there is still an IV hypothesized to have an effect on a DV, the study can be classified as being quasi -experimental.
If something is quasi it means that it’s apparently something, or seems to be something, but it’s not quite. So a quasi-experiment appears to be an experiment, but it’s “not quite.”
This means that sometimes to determine if a study is quasi-experiment or a true experiment, you have to dig deep into the methodology.
A good example to compare a true experiment and a quasi-experiment is by looking at two very similar experiments ( summaries available here ):
Lazar et al. (2005) on the effects of meditation on the brain
Desbordes et al. (2005)on the effects of mindfulness on brain activity.
In Lazar’s experiment they compared the brains of meditation experts with a control group of participants that had no meditation experience. In this case, the researches could not randomly assign participants to be an expert or a control.
Since there is still an IV (meditation experience) that is hypothesized to have an effect on a DV (grey matter in the brain), this is an experiment. But because not all conditions of a true experiment can be met (in this case, there can be no random allocation), we can classify this as a quasi – experiment.
Desbordes et al. studied mindfulness (a type of meditation) on the activity in the brain but this is a true experiment because they controlled for extraneous variables and randomly assigning participants to the treatment and control groups (You can read more about this study here ).
These two studies work well together and can be partnered up to discuss a range of topics, including:
- The use of technological techniques
- Neuroplasticity
- cognitive processes
Traditionally “the experimental method” (which includes true, quasi, natural and field experiments) has been classified as one research method by the IB. This means that if you are asked an essay question to discuss or evaluate the use of one research method, you could identify the experimental method as your method, and include these two studies in your answer. The contrast between quasi and true experimental design could work well for the discussion or evaluation part of the answer.
Travis Dixon is an IB Psychology teacher, author, workshop leader, examiner and IA moderator.

COMMENTS
Quasi-Experimental Design. !If no manipulation is performed on the IV, the design is correlational. !If the IV is manipulated, but there is not complete random assignment to conditions, the design is called quasi-experimental.
The independent variable (IV) is the factor you aim to study or manipulate in your research. Unlike controlled experiments, where you can directly manipulate the IV, quasi-experimental design often deals with naturally occurring variables.
Like a true experiment, a quasi-experimental design aims to establish a cause-and-effect relationship between an independent and dependent variable. However, unlike a true experiment, a quasi-experiment does not rely on random assignment. Instead, subjects are assigned to groups based on non-random criteria.
Example: Quasi-experimental design. You study whether gender identity affects neural responses to infant cries. Your independent variable is a subject variable, namely the gender identity of the participants. You have three groups: men, women and other. Your dependent variable is the brain activity response to hearing infant cries.
Independent variable (IV): The variable that is implied (quasi-experiment, non-experiment) or demonstrated to be (experiment) the cause of an effect. When there is a manipulation, the variable that is manipulated is the IV.
Quasi-experiments contain a naturally occurring IV. However, in a quasi-experiment the naturally occurring IV is a difference between people that already exists (i.e. gender, age). The researcher examines the effect of this variable on the dependent variable (DV).
A quasi experimental design is a method for identifying causal relationships that does not randomly assign participants to the experimental groups. Instead, researchers use a non-random process. For example, they might use an eligibility cutoff score or preexisting groups to determine who receives the treatment.
So if there is no random allocation, but there is still an IV hypothesized to have an effect on a DV, the study can be classified as being quasi-experimental. If something is quasi it means that it’s apparently something, or seems to be something, but it’s not quite.
Quasi experiments have independent variables that already exist such as age, gender, eye color. These variables can either be continuous (age) or they can be categorical (gender). In short, naturally occurring variables are measured within quasi experiments.
It’s a quasi -experiment if it includes at least one SV that is going to be treated as if it were an IV; it’s a correlational study if all of the variables are either DVs or SVs being treated as covariates.