spezifische ladung eines elektrons experiment

Die spezifische Ladung eines Elektrons - e/m Bestimmung

Schlagwörter: e/m spezifische Ladung Elektron, Elektronen wiegen, Lorentzkraft, Magnetfeld, Kreisbahn, Fadenstrahlrohr, Fadenstrahl Röhre, Helmholtz Spulen Paar

Welche Masse hat ein Elektron?

Wenn wir die Ladung eines Elektrons kennen, dann können wir mit dem folgenden Experiment Elektronen „wiegen“.

Eine Waage ist dafür aber sicher kein geeignetes Gerät.

Historisch ist man an das Experiment so herangegangen, dass der Quotient e/m bestimmt wurde. Das ist die spezifische Ladung eines Elektrons.

Vorbetrachtungen zum Experiment

Auf bewegte Ladungsträger (Elektronen) wirkt im Magnetfeld eine Kraft, die LORENTZkraft .

Die Elektronen verlassen die Elektronenkanone mit der konstanten Geschwindigkeit v .

Nach dem NEWTONschen Trägheitsgesetz ändert ein Körper seine Bewegung, wenn eine Kraft auf ihn wirkt. 

Nach der linken-Hand-Regel , wird das Elektron in Richtung der Kreismitte abgelenkt. Dabei ändert sich seine Bewegungsrichtung. Dadurch entsteht (für eine hinreichend große Ablenkung) eine Kreisbahn.

Versuchsidee

Beschleunigte Elektronen werden im Magnetfeld abgelenkt. Wenn die Ablenkung so stark ist, dass sich eine Kreisbahn bildet, dann können durch geschickte Verknüpfungen ( Energieerhaltung , Kraftwirkungen) Aussagen zur Ladung und zur Masse gemacht werden.

Kernstück des Experimentes ist die Fadenstrahlröhre . In der Fadenstrahlröhre befindet sich eine Elektronenkanone (Wehnelt-Zylinder ) in der die Elektronen auf eine bestimmte Geschwindigkeit beschleunigt werden.

Die Röhre befindet sich zwischen einem Helmholtz-Spulenpaar . Die besondere Eigenschaft der Helmholtz Spule ist, dass das Magnetfeld zwischen den Spulen nahezu als homogen betrachtet werden kann.

Auf bewegte Ladungsträger, hier Elektronen, wirkt im Magnetfeld die Lorentzkraft . Bei richtiger Polung werden die Elektronen auf eine Kreisbahn abgelenkt. Im Innenraum der Röhre befinden sich fluoreszierende Reiter, mit deren Hilfe der Radius der Kreisbahn besser abgelesen werden kann. Der Spulenstrom und somit die Stärke des Magnetfelds kann über das Potentiometer geregelt werden. Spulenstrom und Beschleunigungsspannung sind über ein Amperemeter und ein Voltmeter abzulesen.

Beobachtungen

Die beschleunigten Elektronen verlassen mit der Geschwindigkeit v die Elektronenkanone. Nach Verlassen der Elektronenkanone bewegen sich die Elektronen gradlinig ,mit der konstanten Geschwindigkeit v. Es gilt: v=f(U B )

{\large v=\,\sqrt{\frac{2\cdot e\cdot {{U}_{B}}}{{{m}_{e}}}} }

• zur Herleitung der Gleichung

Ein Spulenstrom wird angelegt

Entstehung der Kreisbahn - Kräfte

Die LORENTZkraft F L wirkt hier als Zentripetalkraft F z .

Wir gehen zunächst von einer Bewegung der Elektronen, senkrecht zu den magnetischen Feldlinien aus. { \vec{v}\,\bot \vec{B}\,}

F L bzw. F Z ist stets zum Kreismittelpunkt gerichtet.

{ \begin{array}{l}{{F}_{L}}=e\cdot v\cdot B\,\,\left( \vec{e}\bot \vec{B} \right)\\{{F}_{Z}}=\frac{{{m}_{e}}\cdot {{v}^{2}}}{r}\end{array}  }  

Herleitung – spez. Ladung eines Elektrons e/m

Auf bewegte Ladungen wirkt im Magnetfeld die LORENTZ Kraft.

Die Kraft ist zum Kreismittelpunkt gerichtet. Die Lorentzkraft wirkt als Zentripetalkraft.

{\large q\cdot B\cdot v\,\,=\,\frac{m\cdot {{v}^{2}}}{r}}

Da es sich bei den bewegten Ladungen um Elektronen handelt, können wir die Gleichung konkretisieren. ( q=e; m=m e )

{\large\displaystyle \begin{array}{l}e\cdot B\cdot v\,\,=\,\frac{{{m}_{e}}\cdot {{v}^{2}}}{r}\,\,\,\,\,\,\,\left| :v \right.\\\\e\cdot B\,\,\,\,\,\,=\,\frac{{{m}_{e}}\cdot v}{r}\,\,\,\,\,\left| :{{m}_{e}}\,\,\left| :B \right. \right.\\\\\frac{e}{{{m}_{e}}}\,\,\,\,\,\,\,=\,\,\frac{v}{B\,\cdot \,r}\,\,\,\,\,\,\,\,\,\,Einsetzen\,\,von\,\,v\,\,(1)\\\\\frac{e}{{{m}_{e}}}\,\,\,\,\,\,\,\,=\,\,\frac{\sqrt{\frac{2\cdot e\cdot {{U}_{B}}}{{{m}_{e}}}}}{B\cdot \,r}\,\,\,\,\,\,quadrieren\\\\\frac{{{e}^{2}}}{{{m}_{e}}^{2}}\,\,\,\,\,\,=\,\frac{2\,\cdot \,e\,\cdot \,{{U}_{B}}}{{{m}_{e}}\,\cdot {{B}^{2}}\,\cdot \,{{r}^{2}}}\,\,\,\,\,\left| :\,\frac{e}{{{m}_{e}}} \right.\\\\\,\,\,\huge\frac{e}{{{m}_{e}}}\,\,\,\,\,=\,\,\frac{2\,\cdot \,{{U}_{B}}}{{{B}^{2}}\,\cdot \,{{r}^{2}}}\end{array}  }

Bestimmung der mag. Flussdichte

Statt mit einer HALL-Sonde können wie die Stärke des Magnetfeldes (magnetische Flussdichte B) auch über den Spulenstrom berechnen.

Die Herstellerangebe für das hier verwendete HELMHOLTZ-Spulenpaar lautet:

{\large {{B}_{Helmholtz}}\,=\,{{\mu }_{0}}\,\cdot \,\frac{I\,\cdot \,N}{r}\,\cdot \left( 0,715 \right)}

Bei der 0,715 handelt es sich um einen spulenspezifischen Korrekturfaktor .

Um einen gleichen Strom durch beide Spulen zu gewährleisten, sollten diese in Reihe geschaltet werden.

Die folgenden Messwerte wurden real am 04.12.19 im Unterricht aufgenommen. Die grün unterlegten Werte sind Messwerte. Bei den beige unterlegten Werten handelt es sich um berechnete Werte.

{\large \displaystyle {{B}_{Helmholtz}}={{\mu }_{0}}\cdot \frac{I\cdot N}{R}\cdot (0,715)}

{ \large \displaystyle \frac{e}{m}=\frac{2\cdot U}{{{B}^{2}}\cdot {{r}^{2}}}}

Beispiel : r =5  cm =0,05  m ; U =150  V ; I =1,1 A ; R=20 cm

• Berechnung der magnetischen Flussdichte B

{ \large \displaystyle \begin{array}{l}{{B}_{Helmholtz}}={{\mu }_{0}}\cdot \frac{I\cdot N}{R}\cdot (0,715)\\\\{{B}_{Helmholtz}}\left( 1,1\,A \right)=1,26\cdot {{10}^{-6}}\,\frac{Tm}{A}\cdot \frac{1,1\,A\cdot 154}{0,20\,m}\cdot (0,715)\\\\{{B}_{Helmholtz}}\left( 1,1\,A \right)=7,6\cdot {{10}^{-4}}\,\frac{\text{Tm}}{\text{A}}\cdot \frac{\text{A}}{\text{m}}\,=\,7,6\cdot {{10}^{-4}}\,T\,=\,0,76\,\text{mT}\end{array}}

• Berechnung der spezifischen Ladung e/m

{\large \displaystyle \begin{array}{l}\frac{e}{m}=\frac{2\cdot U}{{{B}^{2}}\cdot {{r}^{2}}}\\\\\frac{e}{m}=\frac{2\cdot 150\,V}{{{\left( 7,6\cdot {{10}^{-4}}\,T \right)}^{2}}\cdot {{\left( 0,05\,m \right)}^{2}}}\\\\\frac{e}{m}=\,2,1\cdot {{10}^{11}}\frac{\,V}{{{T}^{2}}\cdot {{m}^{2}}}\end{array} }

Einheitenbetrachtung:

Die experimentell bestimmte spezifische Ladung des Elektrons beträgt  { 2,1\,\cdot \,{{10}^{11}}\,\frac{C}{kg}}

Bei einer Elementarladung von e =1,6·10 -19  C lässt sich die Masse des Elektrons berechnen.

{\large\begin{array}{l}{{m}_{e}}\,=\,\frac{1}{\left\{ \frac{e}{m} \right\}}\,\cdot e\\{{m}_{e}}\,=\,\frac{1\,\,kg}{2,1\cdot {{10}^{11}}\,C}\,\cdot \,1,6\cdot {{10}^{-19}}\,C\\\\{{m}_{e}}\,=\,7,6\cdot {{10}^{31}}\,kg\end{array} }

Laut Literatur beträgt die Elektronenmasse 9,1·10 -31  kg.

Abweichung bzw. Fehler:

{\large \begin{array}{l}\Delta {{m}_{e}}\,=\,\left| {{m}_{e,lit}}\,-\,{{m}_{e,exp}} \right|\,=\,1,5\cdot {{10}^{-31}}\,kg\\\\relativer\,\,Fehler:\frac{\Delta {{m}_{e}}}{{{m}_{e,lit}}}\,=\,\frac{1,5\cdot {{10}^{-31}}\,kg}{9,1\cdot {{10}^{-31}}\,kg}=\,0,1648\,\approx ,017\end{array}  }

Der relative Fehler beträgt 0,17 bzw. 17 %. Achtung! Beim Runden von Fehlern gelten nicht die mathematischen Rundungsregeln. Fehler werden immer aufgerundet.

Fehlerbetrachtung

Im betrachteten Beispiel lag die Abweichung vom Literaturwert bei 17 %. Die anderen Messwerte liefern Fehler zwischen 14 % und 24 %.

• Können wir mit den Werten zufrieden sein?
• Können wir Änderungen am Versuchsaufbau vornehmen, um den Fehler zu minimieren?

Um das zu überprüfen, führen wir eine Fehlerrechnung durch. Da hier mehrere Messwerte mit ihren Fehlern in die Rechnung eingehen, müssen wir die Regeln der Fehlerfortpflanzung beachten.

Folgende Werte gehen in die Berechnung ein:

• Radius der Elektronenbahn r
• Beschleunigungsspannung U
• magnetische Flussdichte B (Diese werden wir wie den gemessenen Spulenstrom I behandeln, da die Flussdichte direkt aus dem Spulenstrom berechnet wurde.)

zum Radius der Elektronenbahn

Wir schätzen ab, dass wir den Radius mit einer Genauigkeit von 1  mm ablesen können. Damit beträgt der absolute Fehler des Radius Δr =1 mm

zur Beschleunigungsspannung U

Der Fehler der Spannungsmessung setzt sich aus zwei Fehlern zusammen, dem Ablesefehler und dem Fehler des Messgerätes.

Ablesefehler:  Den Ablesefehler im Messbereich 300 V schätzen wir auf 5 V.

Fehler des Messgerätes:  Der Fehler des Messgerätes ergibt sich aus der Güte. Die Güte des Messgerätes gibt den Fehler in Prozenten vom Vollausschlag an. Die Güte beträgt beim verwendeten Messgerät 1,5. 1,5 % von 300 V ergeben einen Fehler von 4,5 V der durch das Messgerät bedingt ist.

Die beiden absoluten Fehler (Ablesefehler und Fehler des Messgerätes) werden addiert. 5 V+4,5 V=9,5 V

Damit beträgt der absolute Fehler der Spannungsmessung ΔU =9,5 V

zur magnetischen Flussdichte

Wie bereits beschrieben, werden wir hier die Strommessung zu Grunde legen. Der Fehler der Strommessung setzt sich aus zwei Fehlern zusammen, dem Ablesefehler und dem Fehler des Messgerätes.

Ablesefehler:  Den Ablesefehler im Messbereich 3 A schätzen wir auf 0,1 A.

Fehler des Messgerätes:  Der Fehler des Messgerätes ergibt sich aus der Güte. Die Güte des Messgerätes gibt den Fehler in Prozenten vom Vollausschlag an. Die Güte beträgt beim verwendeten Messgerät 1,5. 1,5 % von 3 A ergeben einen Fehler von 0,045 A der durch das Messgerät bedingt ist.

Die beiden absoluten Fehler (Ablesefehler und Fehler des Messgerätes) werden addiert. 0,1 A+0,045 A=0,145 A

Damit beträgt der absolute Fehler der Strommessung ΔI=0,145 A

Wie gehen die Messwerte und ihre Fehler in die Berechnung ein?

{\large \displaystyle \frac{e}{m}=\frac{2\cdot U}{{{B}^{2}}\cdot {{r}^{2}}}}

Die Spannung geht mit dem Faktor 2, also quasi als Summe in die Berechnung ein (2·U=U+U)

Die magnetische Flussdichte (bzw. der Spulenstrom) und der Radius der Elektronenbahn gehen jeweils quadratisch in die Berechnung ein.

Die Regeln der Fehlerfortpflanzung zeigen:

• Gehen zwei fehlerbehaftete Größen a und b als Produkt (a·b) oder als Quotient (a/b) in eine Rechnung ein, so ist der relative Fehler des Produktes bzw. des Quotienten gleich der Wurzel, aus den Quadraten der relativen Fehler .
• Geht eine fehlerbehaftete Größe a in der n-ten Potenz in eine Rechnung ein, so ist der relative Fehler der Potenz gleich das n-fache des relativen Fehlers .

{\large \begin{array}{l}\frac{\Delta r}{r}=\,\frac{0,1\,cm}{5\,cm}\,=\,0,02\\\\\frac{\Delta U}{U}\,=\,\frac{9,5\,V\,+\,9,5\,V}{150\,V}\,=\,0,127\\\\\frac{\Delta I}{I}\,=\,\frac{0,145\,A}{1,1\,A}\,=\,0,132\end{array} }

{\large \displaystyle \begin{array}{l}\frac{\Delta \left( \frac{e}{m} \right)}{\left( \frac{e}{m} \right)}\,=\,\sqrt{{{\left( \frac{\Delta U}{U} \right)}^{2}}\,+\,{{\left( 2\cdot \frac{\Delta I}{I} \right)}^{2}}+{{\left( 2\cdot \frac{\Delta r}{r} \right)}^{2}}}\\\\\frac{\Delta \left( \frac{e}{m} \right)}{\left( \frac{e}{m} \right)}\,=\,\sqrt{{{\left( 0,127 \right)}^{2}}\,+\,{{\left( 2\cdot 0,145 \right)}^{2}}+{{\left( 2\cdot 0,02 \right)}^{2}}}\end{array} }

Die Berechnung liefert:

{\large\displaystyle \frac{\Delta \left( \frac{e}{m} \right)}{\left( \frac{e}{m} \right)}\,=\,0,317  }

Damit können wir ein Vertrauensintervall angeben. Das ist der Bereich, in dem sich unsere berechneten Werte auf Basis der Messparameter befinden dürfen.

Dieses Intervall haben wir mit 32 % berechnet.

Wir hatten die spezifische Ladung des Elektrons e/m mit  {\large \displaystyle \frac{e}{m}=\,2,1\cdot {{10}^{11}}\frac{\,C}{kg}  }  berechnet.

Literaturwert:   {\large \displaystyle \frac{e}{m}=\,1,758\,820\cdot {{10}^{11}}\frac{\,C}{kg}  }

32 % von 2,1·10 11  C/kg =0,672  C/kg

{\large\begin{array}{l}\frac{e}{m}=\left( 2,1\,\pm 0,67 \right)\cdot {{10}^{11}}\,\frac{C}{kg}\\bzw.\\\frac{e}{m}=\left( 2,1\,\pm 32\,\% \right)\cdot {{10}^{11}}\,\frac{C}{kg}\end{array} }

Damit können wir feststellen, dass der Literaturwert im berechneten Vertrauensintervall liegt.

Ein Fehler von 32 % sieht auf den ersten Blick nicht wirklich gut aus. Können wir die Messung optimieren?

Dazu ist es hilfreich, sich anzusehen, welche Messung wie stark in die Fehlerrechnung eingeht.

Den größten Fehlereinfluss liefert hier die Strommessung. Wenn wir Werte nahe der Messbereichsgrenze (3  A ) messen, dann reduziert sich der Fehler des Messgerätes deutlich.

Die folgende Tabelle zeigt die Fehlerberechnungen und die Vertrauensbereiche für die vorangestellten Messungen.

Verdrehen der Röhre

Was passiert, wenn die Fadenstrahlröhre verdreht wird?

Die Bewegungsrichtung der Elektronen und die Feldlinien des Magnetfeldes stehen nicht mehr senkrecht zueinander.

… in Arbeit …

• Schülerlexikon
• Physik Abitur
• 4 Elektrizitätslehre und Magnetismus
• 4.2 Das magnetische Feld
• 4.2.3 Geladenen Teilchen und Stoffe in magnetischen Feldern

e/m-Bestimmung

Die spezifische Ladung eines Elektrons ist der Quotient aus der Elementarladung e und der seiner Masse m . Es ist eine wichtige Naturkonstante, die nach CODATA (Committee on Data for Science and Technology) folgenden Wert hat: e m e = 1,758   820 ⋅ 10 11   C ⋅ kg -1 Die spezifische Ladung eines Elektrons kann in unterschiedlicher Weise experimentell bestimmt werden. Das ist selbst mit schulischen Mitteln möglich.

Bild 1 zeigt eine Versuchsanordnung mit einem Fadenstrahlrohr.

Versuchsanordnung zur Bestimmung der spezifischen Ladung von Elektronen

Bestimmung der spezifischen Ladung mit dem Fadenstrahlrohr

Eine relativ einfache Bestimmung der grundlegenden Naturkonstanten e/m zu kann mithilfe eines sogenannten Fadenstrahlrohr es erfolgen. Das ist eine kugelförmige evakuierte Röhre mit einem Füllgas, einer heizbaren Katode und einer Anode. Durch die Katode werden Elektronen emittiert, durch eine Spannung zwischen Katode und Anode beschleunigt und durch Blenden ein feiner Strahl, ein Elektronenstrahl , ausgeblendet. Durch Ionisation des Füllgases wird die Bahn des Elektronenstrahls sichtbar. Bringt man das Fadenstrahlrohr so in ein homogenes Magnetfeld , dass die Bewegungsrichtung der Elektronen und die Richtung des Magnetfeldes senkrecht zueinander sind, dann wirkt die LORENTZ-Kraft als Radialkraft . Die Elektronen bewegen sich auf einer Kreisbahn (Bild 2). Das erforderliche homogene Magnetfeld erzeugt man durch HELMHOLTZ-Spulen .

Da die Radialkraft die LORENTZ-Kraft ist, kann man setzen:

Radialkraft = LORENTZ-Kraft m ⋅ v 2 r = e ⋅ v ⋅ B Die Divion durch v ergibt: m ⋅ v r = e ⋅ B (1) Die Geschwindigkeit v ergibt sich aus der Beschleunigungsspannung zwischen Katode und Anode zu: v = 2   U ⋅ e m (2) Setzt man (2) in (1) ein , so erhält man: m ⋅ 2   U ⋅ e m r = e ⋅ B Quadrieren der Gleichung ergibt: m 2 ⋅ 2   U ⋅ e r 2 ⋅ m = e 2 ⋅ B 2 oder m ⋅ 2   U r 2 = e ⋅ B 2 Durch Umstellen nach der spezifischen Ladung erhält man: e m = 2   U r 2 ⋅ B 2 U Beschleunigungsspannung (Spannung zwischen Katode und Anode) r Radius der Kreisbahn B magnetische Flussdichte im Feld der HELMHOLTZ-Spulen

Alle rechts stehenden Größen sind messbar, damit die spezifische Ladung experimentell ermittelbar. Die magnetische Flussdichte kann man aus den Abmessungen der HELMHOLTZ-Spulen, ihrer Windungszahl und der Stromstärke in ihnen berechnen oder mit einer HALL-Sonde direkt messen.

Im homogenen Magnetfeld von HELMHOLTZ-Spulen bewegen sich die Elektronen des Elektronenstrahls auf einer Kreisbahn.

Bestimmung der spezifischen Ladung mit einer Katodenstrahlröhre

Eine andere Möglichkeit der Bestimmung der spezifischen Ladung von Elektronen besteht darin, mit einer Katodenstrahlröhre (braunsche Röhre) einen Elektronenstrahl zur erzeugen (Bild 3) und diesen Elektronenstrahl einem homogenen Magnetfeld auszusetzen, wobei auch hier die Bewegungsrichtung der Elektronen und die Feldrichtung senkrecht zueinander sind. Das homogene Magnetfeld kann das zwischen HELMHOLTZ-Spulen sein. Man kann aber auch das relativ schwache und in einem kleinen Raumbereich konstante Magnetfeld der Erde nutzen. Dann müsste man folgendermaßen vorgehen:

• Die Katodenstrahlröhre wird horizontal befestigt. Da ferromagnetische Stoffe die Messung beeinflussen, müssen Halterungen aus Aluminium oder Holz verwendet werden.
• Mithilfe eines Kompasses wird die Längsachse der Röhre in Nord-Süd-Richtung ausgerichtet und die Röhre in Betrieb genommen. Die Bewegungsrichtung der Elektronen stimmt dann mit der Richtung des Magnetfeldes überein. Die Elektronen werden demzufolge durch das Magnetfeld nicht beeinflusst. Mit Filzstift wird ein markanter Punkt des Leuchtflecks auf dem Leuchtschirm markiert.
• Anschließend wird die Röhre in Ost-West-Richtung bzw. in West-Ost-Richtung gedreht und jeweils der gleiche Punkt des Leuchtflecks markiert. Der Abstand zwischen diesen beiden Punkten (2s) wird gemessen.

Einfache Katodenstrahlröhre

Aus der Ablenkung s und dem Abstand zwischen Anode und Leuchtschirm kann man den Radius der Kreisbahn ermitteln (Bild 4). Nach dem Satz von PYTHAGORAS gilt: r 2 = l 2 + ( r − s ) 2 Auflösen der Klammer und Umstellen nach dem Radius ergibt: r = l 2 2   s + s 2

Kennt man den Radius, so kann man zur Berechnung der spezifischen Ladung die oben genannte Gleichung e m = 2   U r 2 ⋅ B 2 nutzen. U ist die zwischen Katode und Anode anliegende Beschleunigungsspannung. Die magnetische Flussdichte des Erdmagnetfeldes kann man Tabellen entnehmen oder direkt messen.

Hinweis: Die Ablenkung von Elektronen in elektrischen Feldern ist nicht zur e/m -Bestimmung geeignet, da sie von der spezifischen Ladung unabhängig ist.

Bestimmung des Radius der Kreisbahn aus der Ablenkung s

Stand: 2010 Dieser Text befindet sich in redaktioneller Bearbeitung.

Mit deinem persönlichen Nachhilfe-Tutor Kim & Duden Learnattack checkst du alles. Jetzt 30 Tage risikofrei testen.

• KI-Tutor Kim hilft bei allen schulischen Problemen
• Individuelle, kindgerechte Förderung in Dialogform
• Lernplattform für 9 Fächer ab der 4. Klasse
• Über 40.000 Erklärvideos, Übungen & Klassenarbeiten
• Rund um die Uhr für dich da

Rechtliches

• Sicherheit & Datenschutz
• Neues Passwort anfordern

• Schulfächer
• Muster-Lösungen
• Frage stellen
• Neu registrieren
• Facharbeiten
• Alle Schulfächer
• Tipps & Tricks
• Über uns

Die experimentelle Bestimmung der spezischen Ladung e/m eines Elektrons

Versuchsanalyse im leistungskurs physik.

• Bewertung 4 von 5 auf Basis von 22 Stimmen
• Elektronik und Beschleunigung: Zusammenfassung für die Mittelstufe
• Referat ----> Spezifische Ladung des Elektrons <---- (0 Antworten)
• Ruhemasse eines Elektrons& spezifische Ladung eines Myons (1 Antworten)
• myonen (2 Antworten)
• Bestimmung der Masse des Elektrons (13 Antworten)
• elektrizität (6 Antworten)
• Elektronik und Beschleunigung: Zusammenfassung für die Mittelstufe Es ist eine Zusammenfassung von der Elektronik. Es kommen die wichtigsten Formel und Definitionssätze vor. Das Gleiche gilt für ..
• Referat ----> Spezifische Ladung des Elektrons <---- Moin, muss in Physik nen Referat über ---> Spezifische Ladung des Elektrons <----- halten könnt ihr mir helfen wa sich da ..
• Ruhemasse eines Elektrons& spezifische Ladung eines Myons Hallo, leider bin ich eine absolute Physik niete... Daher habe ich 2 Fragen: 1:Wie berechne ich die spezifische Ladung eines ..
• myonen In myonien (dort gibt es keine elektronen sonderne myonen, die aber auch die ladung -e haben) wird der versuch zur bestimmung ..
• Bestimmung der Masse des Elektrons m= (e*r^2*b^2)/(2U) Ich hab die einzelnen Variablen: I = 1,6A r= 3cm U = 110 m = (e* 0,03^2m * 1,6^2A)/(220) Doch ..
• elektrizität hallo was hat elektrizität mit physik zu tun

• HÄUFIGE FRAGEN
• RECHTLICHE HINWEISE
• DATENSCHUTZ
• DATENSCHUTZEINSTELLUNGEN
• ÜBER UNS

• e/m-Bestimmung
• spezifische Ladung

• Anwendungen

$\Rightarrow v_0=\,$ ${5.930\cdot 10^6}$ $\frac{\text m}{\text s}$

$\Rightarrow B=\,$ ${0}$ $\text {T}$

schematische Darstellung:

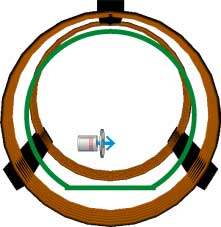
Aufgabe: Bestimme mithilfe des Experimentes e/m.