Worked out Problems on Ratio and Proportion
Worked out problems on ratio and proportion are explained here in detailed description using step-by-step procedure. Solved examples involving different questions related to comparison of ratios in ascending order or descending order, simplification of ratios and also word problems on ratio proportion. Sample questions and answers are given below in the worked out problems on ratio and proportion to get the basic concepts of solving ratio proportion.
1. Arrange the following ratios in descending order.
2 : 3, 3 : 4, 5 : 6, 1 : 5 Solution: Given ratios are 2/3, 3/4, 5/6, 1/5 The L.C.M. of 3, 4, 6, 5 is 2 × 2 × 3 × 5 = 60
Now, 2/3 = (2 × 20)/(3 × 20) = 40/60 3/4 = (3 × 15)/(4 × 15) = 45/60 5/6 = (5 × 10)/(6 × 10) = 50/60 1/5 = (1 × 12)/(5 × 12) = 12/60 Clearly, 50/60 > 45/60 > 40/60 > 12/60 Therefore, 5/6 > 3/4 > 2/3 > 1/5 So, 5 : 6 > 3 : 4 > 2 : 3 > 1 : 5
2. Two numbers are in the ratio 3 : 4. If the sum of numbers is 63, find the numbers. Solution: Sum of the terms of the ratio = 3 + 4 = 7 Sum of numbers = 63 Therefore, first number = 3/7 × 63 = 27 Second number = 4/7 × 63 = 36 Therefore, the two numbers are 27 and 36.
3. If x : y = 1 : 2, find the value of (2x + 3y) : (x + 4y) Solution: x : y = 1 : 2 means x/y = 1/2 Now, (2x + 3y) : (x + 4y) = (2x + 3y)/(x + 4y) [Divide numerator and denominator by y.] = [(2x + 3y)/y]/[(x + 4y)/2] = [2(x/y) + 3]/[(x/y) + 4], put x/y = 1/2 We get = [2 (1/2) + 3)/(1/2 + 4) = (1 + 3)/[(1 + 8)/2] = 4/(9/2) = 4/1 × 2/9 = 8/9 Therefore the value of (2x + 3y) : (x + 4y) = 8 : 9
More solved problems on ratio and proportion are explained here with full description.
4. A bag contains $510 in the form of 50 p, 25 p and 20 p coins in the ratio 2 : 3 : 4. Find the number of coins of each type.
Solution: Let the number of 50 p, 25 p and 20 p coins be 2x, 3x and 4x. Then 2x × 50/100 + 3x × 25/100 + 4x × 20/100 = 510 x/1 + 3x/4 + 4x/5 = 510 (20x + 15x + 16x)/20 = 510 ⇒ 51x/20 = 510 x = (510 × 20)/51 x = 200 2x = 2 × 200 = 400 3x = 3 × 200 = 600 4x = 4 × 200 = 800. Therefore, number of 50 p coins, 25 p coins and 20 p coins are 400, 600, 800 respectively.
5. If 2A = 3B = 4C, find A : B : C Solution: Let 2A = 3B = 4C = x So, A = x/2 B = x/3 C = x/4 The L.C.M of 2, 3 and 4 is 12 Therefore, A : B : C = x/2 × 12 : x/3 × 12 : x/4 = 12 = 6x : 4x : 3x = 6 : 4 : 3 Therefore, A : B : C = 6 : 4 : 3
6. What must be added to each term of the ratio 2 : 3, so that it may become equal to 4 : 5? Solution: Let the number to be added be x, then (2 + x) : (3 + x) = 4 : 5 ⇒ (2 + x)/(5 + x) = 4/5 5(2 + x) = 4(3 + x) 10 + 5x = 12 + 4x 5x - 4x = 12 - 10 x = 2
7. The length of the ribbon was originally 30 cm. It was reduced in the ratio 5 : 3. What is its length now? Solution: Length of ribbon originally = 30 cm Let the original length be 5x and reduced length be 3x. But 5x = 30 cm x = 30/5 cm = 6 cm Therefore, reduced length = 3 cm = 3 × 6 cm = 18 cm
More worked out problems on ratio and proportion are explained here step-by-step. 8. Mother divided the money among Ron, Sam and Maria in the ratio 2 : 3 : 5. If Maria got $150, find the total amount and the money received by Ron and Sam. Solution: Let the money received by Ron, Sam and Maria be 2x, 3x, 5x respectively. Given that Maria has got $ 150. Therefore, 5x = 150 or, x = 150/5 or, x = 30 So, Ron got = 2x = $ 2 × 30 = $60 Sam got = 3x = 3 × 60 = $90
Therefore, the total amount $(60 + 90 + 150) = $300
9. Divide $370 into three parts such that second part is 1/4 of the third part and the ratio between the first and the third part is 3 : 5. Find each part. Solution: Let the first and the third parts be 3x and 5x. Second part = 1/4 of third part. = (1/4) × 5x = 5x/4 Therefore, 3x + (5x/4) + 5x = 370 (12x + 5x + 20x)/4 = 370 37x/4 = 370 x = (370 × 4)/37 x = 10 × 4 x = 40 Therefore, first part = 3x = 3 × 40 = $120 Second part = 5x/4 = 5 × 40/4 = $50 Third part = 5x = 5 × 40 = $ 200
10. The first, second and third terms of the proportion are 42, 36, 35. Find the fourth term. Solution: Let the fourth term be x. Thus 42, 36, 35, x are in proportion. Product of extreme terms = 42 ×x Product of mean terms = 36 X 35 Since, the numbers make up a proportion Therefore, 42 × x = 36 × 35 or, x = (36 × 35)/42 or, x = 30 Therefore, the fourth term of the proportion is 30.
More worked out problems on ratio and proportion using step-by-step explanation. 11. Set up all possible proportions from the numbers 8, 12, 20, 30. Solution: We note that 8 × 30 = 240 and 12 × 20 = 240 Thus, 8 × 30 = 12 × 20 ………..(I) Hence, 8 : 12 = 20 : 30 ……….. (i) We also note that, 8 × 30 = 20 × 12 Hence, 8 : 20 = 12 : 30 ……….. (ii) (I) can also be written as 12 × 20 = 8 × 30 Hence, 12 : 8 = 30 : 20 ……….. (iii) Last (I) can also be written as 12 : 30 = 8 : 20 ……….. (iv) Thus, the required proportions are 8 : 12 = 20 : 30 8 : 20 = 12 : 30 12 : 8 = 30 : 20 12 : 30 = 8 : 20
12. The ratio of number of boys and girls is 4 : 3. If there are 18 girls in a class, find the number of boys in the class and the total number of students in the class. Solution: Number of girls in the class = 18 Ratio of boys and girls = 4 : 3 According to the question, Boys/Girls = 4/5 Boys/18 = 4/5 Boys = (4 × 18)/3 = 24 Therefore, total number of students = 24 + 18 = 42.
13. Find the third proportional of 16 and 20. Solution: Let the third proportional of 16 and 20 be x. Then 16, 20, x are in proportion. This means 16 : 20 = 20 : x So, 16 × x = 20 × 20 x = (20 × 20)/16 = 25 Therefore, the third proportional of 16 and 20 is 25.
● Ratio and Proportion
What is Ratio and Proportion?
Practice Test on Ratio and Proportion
● Ratio and Proportion - Worksheets
Worksheet on Ratio and Proportion
8th Grade Math Practice From Worked out Problems on Ratio and Proportion to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments
Share this page: What’s this?
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy

Recent Articles
Worksheet on Addition of Length | Word Problems on Addition of Length
Nov 17, 24 10:29 PM
Worksheet on Addition of Mass | Word problems on Addition of Mass
Nov 17, 24 10:26 PM
Worksheet on Addition of Capacity | Word Problems on Adding capacity
Nov 17, 24 10:19 PM

Subtraction of Capacity | Units of Capacity and Volume | Examples
Nov 17, 24 10:07 PM

Measuring Capacity | Standard Unit of Capacity | Litre | Millilitres
Nov 17, 24 01:37 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.
WORD PROBLEMS ON RATIO AND PROPORTION
Problem 1 :
The average age of three boys is 25 years and their ages are in the proportion 3 : 5 : 7. Find the age of the youngest boy.
From the ratio 3 : 5 : 7, the ages of three boys are 3x, 5x and 7x.
Average age of three boys = 25
(3x + 5x + 7x)/3 = 25
Age of the first boy = 3x
Age of the first boy = 5x
Age of the first boy = 7x
So, the age of the youngest boy is 15 years.
Problem 2 :
John weighs 56.7 kilograms. If he is going to reduce his weight in the ratio 7 : 6, find his new weight.
Given : Original weight of John = 56.7 kg. He is going to reduce his weight in the ratio 7:6.
We can use the following hint to find his new weight, after it is reduced in the ratio 7 : 6.
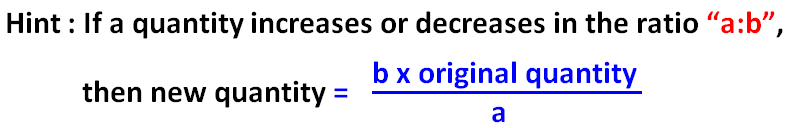
His new weight is
= (6 ⋅ 56.7)/7
So, John's new weight is 48.6 kg.
Problem 3 :
The ratio of the no. of boys to the no. of girls in a school of 720 students is 3 : 5. If 18 new girls are admitted in the school, find how many new boys may be admitted so that the ratio of the no. of boys to the no. of girls may change to 2 : 3.
Sum of the terms in the given ratio is
So, no. of boys in the school is
= 720 ⋅ (3/8)
= 270
No. of girls in the school is
= 720 ⋅ (5/8)
Given : Number of new girls admitted in the school is 18.
Let x be the no. of new boys admitted in the school.
After the above new admissions,
No. of boys in the school = 270 + x
No. of girls in the school = 450 + 18 = 468
Given : The ratio after the new admission is 2 : 3.
Then, we have
(270 + x) : 468 = 2 : 3
Use cross product rule.
3(270 + x) = 468 ⋅ 2
810 + 3x = 936
So, the number of new boys admitted in the school is 42.
Problem 4 :
The monthly incomes of two persons are in the ratio 4 : 5 and their monthly expenditures are in the ratio 7 : 9. If each saves $50 per month, find the monthly income of the second person.
From the given ratio of incomes ( 4 : 5 ),
Income of the 1st person = 4x
Income of the 2nd person = 5x
(Expenditure = Income - Savings)
Then, expenditure of the 1st person = 4x - 50
Expenditure of the 2nd person = 5x - 50
Expenditure ratio = 7 : 9 (given)
So, we have
(4x - 50) : (5x - 50) = 7 : 9
9(4x - 50) = 7(5x - 50)
36x - 450 = 35x - 350
Then, the income of the second person is
So, income of the second person is $500.
Problem 5 :
The ratio of the prices of two houses was 16 : 23. Two years later when the price of the first has increased by 10% and that of the second by $477, the ratio of the prices becomes 11 : 20. Find the original price of the first house.
From the given ratio 16 : 23,
Original price of the 1st house = 16x
Original price of the 2nd house = 23x
After increment in prices,
Price of the 1st house = 16x + 10% of 16x
= 16x + 1.6x
Price of the 2nd house = 23x + 477
After increment in prices, the ratio of prices becomes 11:20.
17.6x : (23x + 477) = 11 : 20
20(17.6x) = 11(23x + 477)
352x = 253x + 5247
Then, original price of the first house is
So, original price of the first house is $848.
Problem 6 :
Two numbers are respectively 20% and 50% are more than a third number, Find the ratio of the two numbers.
Let x be the third number.
Then, the first number is
= (100 + 20)% of x
= 120% of x
The second number is
= (100 + 50)% of x
= 150% of x
The ratio between the first number and second number is
= 1.2x : 1.5x
= 1.2 : 1.5
So, the ratio of two numbers is 4 : 5.
Problem 7 :
The milk and water in two vessels A and B are in the ratio 4:3 and 2:3 respectively. In what ratio, the liquids in both the vessels be mixed to obtain a new mixture in vessel C consisting half milk and half water ?
[4 : 3 ----> 4 + 3 = 7, M ----> 4/7, W ----> 3/7]
Let x be the quantity of mixture taken from vessel A to obtain a new mixture in vessel C.
Quantity of milk in x = (4/7)x = 4x/7
Quantity of water in x = (3/7)x = 3x/7
[2 : 3 ----> 2 + 3 = 5, M ---> 2/5, W ----> 3/5]
Let y be the quantity of mixture taken from vessel B to obtain a new mixture in vessel C.
Quantity of milk in y = (2/5)y = 2y/5
Quantity of water in y = (3/5)y = 3y/5
Vessel A and B :
Quantity of milk from A and B is
= 4x/7 + 2y/5
= (20x + 14y)/35
Quantity of water from A and B is
= (3x/7) + (3y/5)
= (15x + 21y)/35
According to the question, vessel C must consist half of the milk and half of the water.
That is, in vessel C, quantity of milk and water must be same.
There fore,
quantity of milk in (A + B) = quantity of water in (A + B)
(20x + 14y)/35 = (15x + 21y)/35
20x + 14y = 15x + 21y
x : y = 7 : 5
So, the required ratio is 7 : 5.
Problem 8 :
A vessel contains 20 liters of a mixture of milk and water in the ratio 3:2. From the vessel, 10 liters of the mixture is removed and replaced with an equal quantity of pure milk. Find the ratio of milk and water in the final mixture obtained.
[3 : 2 ----> 3 + 2 = 5, M ----> 3/5, W ----> 2/5]
In 20 liters of mixture,
no. of liters of milk = 20 ⋅ 3/5 = 12
no. of liters of water = 20 ⋅ 2/5 = 8
Now, 10 liters of mixture removed.
In this 10 liters of mixture, milk and water will be in the ratio 3 : 2.
no. of liters of milk in this 10 liters = 10 ⋅ 3/5 = 6
no. of liters of water in this 10 liters = 10 ⋅ 2/5 = 4
After removing 10 liters (1st time),
no. of liters of milk in the vessel = 12 - 6 = 6
no. of liters of water in the vessel = 8 - 4 = 4
Now, we add 10 liters of pure milk in the vessel,
After adding 10 liters of pure milk in the vessel,
no. of liters of milk in the vessel = 6 + 10 = 16
no. of liters of water in the vessel = 4 + 0 = 4
After removing 10 liters of mixture and adding 10 liters of pure milk, the ratio of milk and water is
So, the required ratio is 4 : 1.
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents
Recent Articles
Word Problems on Division
Nov 17, 24 01:42 PM
SAT Math Resources (Videos, Concepts, Worksheets and More)
Nov 16, 24 08:15 AM
Digital SAT Math Problems and Solutions (Part - 71)
Nov 16, 24 08:03 AM

IMAGES